Trắc nghiệm Bài 3. Gia tốc và đồ thị vận tốc - thời gian - Vật Lí 10 Cánh diềuĐề bài Câu 1 : Chuyển động thẳng là chuyển động có quỹ đạo là đường gì?
Câu 2 : Khi nào thì độ dịch chuyển và quãng đường bằng nhau?
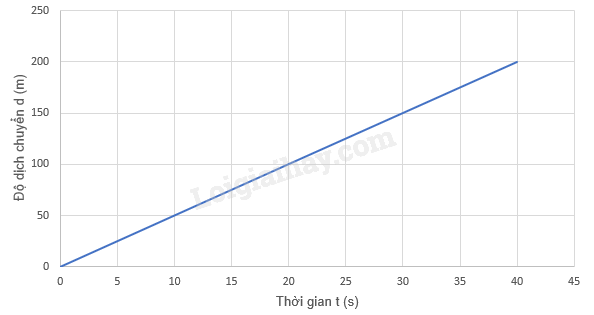
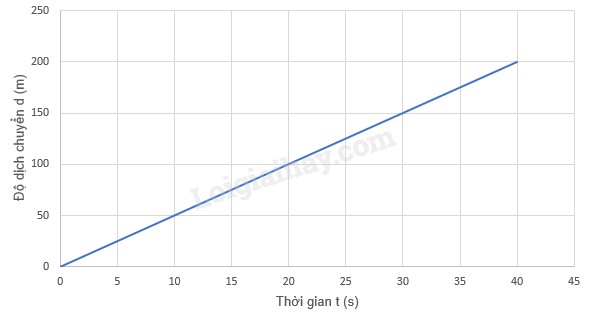
Câu 4 : Cho đồ thị độ dịch chuyển – thời gian sau, độ dịch chuyển của vật trong 25 s đầu tiên là bao nhiêu?
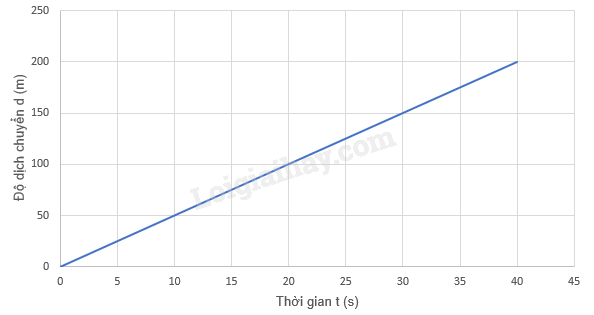
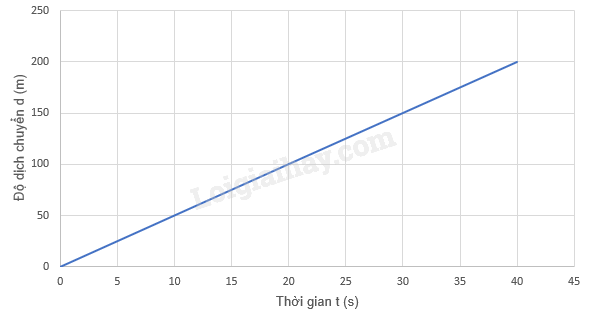
Câu 5 : Cho đồ thị độ dịch chuyển – thời gian sau, độ dịch chuyển của vật từ giây thứ 25 đến giây thứ 30 là bao nhiêu?
Câu 7 : Cho bảng số liệu dưới đây:
Vận tốc của vật trong chuyển động trong 10 s đầu là?
Câu 8 : Cho bảng số liệu dưới đây:
Vận tốc của vật trong chuyển động từ giây thứ thứ 25 đến giây 40 là bao nhiêu?
Câu 9 : Gia tốc là đại lượng vật lý đặc trưng cho
Câu 10 : Gia tốc của vật được xác định bởi biểu thức:
Câu 11 : Chọn đáp án đúng về chuyển động biến đổi
Câu 12 : Chuyển động nhanh dần là chuyển động có:
Câu 13 : Chuyển động chậm dần là chuyển động có:
Câu 14 : Một xe máy đang đi với vận tốc 15 m/s thì thấy có vật cản ở trước mặt thì người đó phanh gấp. Biết khoảng cách kể từ lúc bắt đầu phanh đến chỗ vật cản là 15 m và gia tốc của người này có độ lớn là 5 m/s2 . Hỏi người đó có phanh kịp không, nếu phanh kịp thì khoảng cách từ lúc dừng hẳn đến vật cản là bao nhiêu?
Câu 15 : Một ô tô đang chuyển động với vận tốc 10 m/s thì bắt đầu tăng tốc. Biết rằng sau 10 s kể từ khi tăng tốc, xe đạt vận tốc là 15 m/s. Gia tốc của xe là bao nhiêu?
Câu 16 : Một ô tô bắt đầu xuất phát và chuyển động nhanh dần với gia tốc có độ lớn là 3 m/s2 . Sau 10 s, xe đi được quãng đường là bao nhiêu?
Câu 17 : Một máy bay đang bay với vận tốc là 400 m/s thì chuyển động chậm dần để hạ cánh, 20 giây sau thì máy bay hạ cánh an toàn. Gia tốc của máy bay là:
Lời giải và đáp án Câu 1 : Chuyển động thẳng là chuyển động có quỹ đạo là đường gì?
Đáp án : B Phương pháp giải : Vận dụng kiến thức đã học Lời giải chi tiết : Chuyển động thẳng là chuyển động có quỹ đạo là đường thẳng Câu 2 : Khi nào thì độ dịch chuyển và quãng đường bằng nhau?
Đáp án : A Phương pháp giải : Vận dụng kiến thức đã học Lời giải chi tiết : Khi vật chuyển động thẳng theo một chiều không đổi thì độ dịch chuyển và quãng đường đi được có độ lớn như nhau.
Đáp án : C Phương pháp giải : Cách viết phương trình đường thẳng đi qua gốc tọa độ + Phương trình đường thẳng có dạng: d = a.t + Lấy một tọa độ điểm bất kì trên đồ thị, thay vào phương trình, tìm a + Thay a ngược trở lại phương trình, từ đó suy ra phương trình đường thẳng. Lời giải chi tiết : Gọi phương trình đường thẳng có dạng: d = a.t Khi t = 10 s thì d = 50 m => 50 = a.10 => a = 5 Vậy phương trình đồ thị độ dịch chuyển – thời gian là: d =5t (m). Câu 4 : Cho đồ thị độ dịch chuyển – thời gian sau, độ dịch chuyển của vật trong 25 s đầu tiên là bao nhiêu?
Đáp án : C Phương pháp giải : - Viết phương trình đồ thị độ dịch chuyển – thời gian: + Phương trình đường thẳng có dạng: d = a.t + Lấy một tọa độ điểm bất kì trên đồ thị, thay vào phương trình, tìm a + Thay a ngược trở lại phương trình, từ đó suy ra phương trình đường thẳng. - Thay thời gian t vào phương trình tìm d Lời giải chi tiết : Gọi phương trình đường thẳng có dạng: d = a.t Khi t = 10 s thì d = 50 m => 50 = a.10 => a = 5 Vậy phương trình đồ thị độ dịch chuyển – thời gian là: d = 5t (m). Thay t = 25 s vào phương trình, ta có: d = 5.25 = 125 (m). Câu 5 : Cho đồ thị độ dịch chuyển – thời gian sau, độ dịch chuyển của vật từ giây thứ 25 đến giây thứ 30 là bao nhiêu?
Đáp án : B Phương pháp giải : Độ dịch chuyển bằng khoảng cách điểm đầu và điểm cuối. Lời giải chi tiết : Từ hình vẽ ta có: Tọa độ của vật tại thời điểm 30 s là: 150 m Gọi phương trình đường thẳng có dạng: d = a.t Khi t = 10 s thì d = 50 m => 50 = a.10 => a = 5 Vậy phương trình đồ thị độ dịch chuyển – thời gian là: d =5t (m). Thay t = 25 s vào phương trình, ta có: d = 5.25 = 125 (m). => Tọa độ của vật tại thời điểm 25 s là: 125 m => Độ dịch chuyển d = 150 – 125 = 25 m.
Đáp án : B Phương pháp giải : Vận tốc của chuyển động thẳng đều chính là hệ số góc của đồ thị Lời giải chi tiết : Gọi phương trình đường thẳng có dạng: d = a.t Khi t = 10 s thì d = 50 m => 50 = a.10 => a = 5 Câu 7 : Cho bảng số liệu dưới đây:
Vận tốc của vật trong chuyển động trong 10 s đầu là?
Đáp án : B Phương pháp giải : Biểu thức tính vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}}\) Trong đó: + Δd: độ dịch chuyển (m) + Δt: thời gian dịch chuyển (s) Lời giải chi tiết : Vận tốc của vật trong 10 s đầu là: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{100}}{{10}} = 10(m/s)\) Câu 8 : Cho bảng số liệu dưới đây:
Vận tốc của vật trong chuyển động từ giây thứ thứ 25 đến giây 40 là bao nhiêu?
Đáp án : C Phương pháp giải : Biểu thức tính vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}}\) Trong đó: + Δd: độ dịch chuyển (m) + Δt: thời gian dịch chuyển (s) Lời giải chi tiết : Vận tốc của vật từ giây thứ 25 đến giây thứ 40 là: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{300 - 200}}{{40 - 25}} \approx 6,67(m/s)\) Câu 9 : Gia tốc là đại lượng vật lý đặc trưng cho
Đáp án : D Lời giải chi tiết : Gia tốc là đại lượng vật lý đặc trưng cho khả năng thay đổi vận tốc (cả hướng và độ lớn) của vật và được xác định bằng biểu thức: \(\overrightarrow a = \dfrac{{\overrightarrow v - \overrightarrow {{v_0}} }}{{t - {t_0}}} = \dfrac{{\Delta \overrightarrow v }}{{\Delta t}}\) Câu 10 : Gia tốc của vật được xác định bởi biểu thức:
Đáp án : A Lời giải chi tiết : Gia tốc là đại lượng vật lý đặc trưng cho khả năng thay đổi vận tốc (cả hướng và độ lớn) của vật và được xác định bằng biểu thức: \(\overrightarrow a = \frac{{\overrightarrow v - \overrightarrow {{v_0}} }}{{t - {t_0}}} = \frac{{\Delta \overrightarrow v }}{{\Delta t}}\) Câu 11 : Chọn đáp án đúng về chuyển động biến đổi
Đáp án : C Phương pháp giải : Chuyển động có vận tốc thay đổi được gọi là chuyển động biến đổi. Lời giải chi tiết : Chuyển động có vận tốc thay đổi chỉ có trường hợp của xe máy đang đi trên đường. Câu 12 : Chuyển động nhanh dần là chuyển động có:
Đáp án : C Phương pháp giải : Vận dụng kiến thức đã học Lời giải chi tiết : Chuyển động nhanh dần là chuyển động có a.v > 0 Câu 13 : Chuyển động chậm dần là chuyển động có:
Đáp án : D Phương pháp giải : Vận dụng kiến thức đã học Lời giải chi tiết : Chuyển động chậm dần là chuyển động có a.v < 0 Câu 14 : Một xe máy đang đi với vận tốc 15 m/s thì thấy có vật cản ở trước mặt thì người đó phanh gấp. Biết khoảng cách kể từ lúc bắt đầu phanh đến chỗ vật cản là 15 m và gia tốc của người này có độ lớn là 5 m/s2 . Hỏi người đó có phanh kịp không, nếu phanh kịp thì khoảng cách từ lúc dừng hẳn đến vật cản là bao nhiêu?
Đáp án : D Phương pháp giải : - Biểu thức mối liên hệ giữa vận tốc, gia tốc và quãng đường: \({v^2} - v_0^2 = 2.a.s\) Lời giải chi tiết : Ta có: v0 = 15 m/s; a = - 5 m/s2 ; v = 0 m/s Quãng đường mà người đó đi được kể từ khi phanh gấp là: \({v^2} - v_0^2 = 2.a.s \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2.a}} = \frac{{{0^2} - {{15}^2}}}{{2.( - 5)}} = 22,5(m)\) => s > 15 m => Xe phanh không kịp Câu 15 : Một ô tô đang chuyển động với vận tốc 10 m/s thì bắt đầu tăng tốc. Biết rằng sau 10 s kể từ khi tăng tốc, xe đạt vận tốc là 15 m/s. Gia tốc của xe là bao nhiêu?
Đáp án : B Phương pháp giải : Biểu thức tính gia tốc là: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{v - {v_0}}}{{t - {t_0}}}\) Lời giải chi tiết : Ta có: v = 15 m/s; v0 = 10 m/s; Δt = 10 s => Gia tốc của ô tô là: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{v - {v_0}}}{{t - {t_0}}} = \frac{{15 - 10}}{{10}} = 0,5(m/{s^2})\) Câu 16 : Một ô tô bắt đầu xuất phát và chuyển động nhanh dần với gia tốc có độ lớn là 3 m/s2 . Sau 10 s, xe đi được quãng đường là bao nhiêu?
Đáp án : B Phương pháp giải : Biểu thức tính quãng đường trong chuyển động biến đổi (đối với mốc là lúc vật bắt đầu xuất phát): \(s = {v_0}.t + \frac{1}{2}a{t^2}\) Lời giải chi tiết : Vật bắt đầu xuất phát nên v0 = 0 m/s Ta có a = 3 m/s2 ; t = 10 s => Quãng đường ô tô đi được là: \(s = {v_0}.t + \frac{1}{2}a{t^2} = \frac{1}{2}{.3.10^2} = 150(m)\) Câu 17 : Một máy bay đang bay với vận tốc là 400 m/s thì chuyển động chậm dần để hạ cánh, 20 giây sau thì máy bay hạ cánh an toàn. Gia tốc của máy bay là:
Đáp án : C Phương pháp giải : Biểu thức tính gia tốc là: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{v - {v_0}}}{{t - {t_0}}}\) Lời giải chi tiết : Ta có v = 400 m/s; v0 = 0 m/s; Δt = 20 s Gia tốc của máy bay là: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{v - {v_0}}}{{t - {t_0}}} = \frac{{0 - 400}}{{20}} = - 20(m/{s^2})\)
|