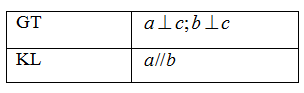Trắc nghiệm Bài 4: Định lí và chứng minh một định lí Toán 7 Chân trời sáng tạo Đề bài - A
Giả thiết của định lý là điều cho biết. - B
Kết luận của định lý là điều được suy ra. - C
Giả thiết của định lý là điều được suy ra. - D
Câu 2 : Định lý sau được phát biểu thành lời là: 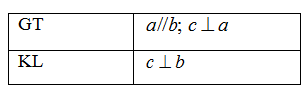 - A
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia. - B
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia. - C
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\) - D
Câu 3 : Phát biểu định lý sau bằng lời: 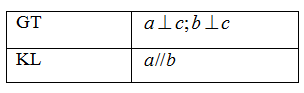 - A
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau. - B
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau. - C
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - D
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Câu 4 : Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là: 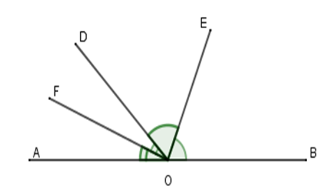 - A
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OF\) - B
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OA\) - C
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\). Kết luận: \(OE \bot OF\) - D
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OB \bot OF\)
Câu 5 : Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là 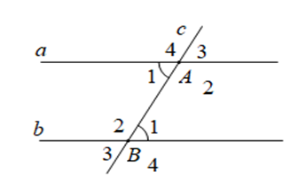 - A
- B
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\) - C
- D
Câu 6 : Trong các câu sau, câu nào cho một định lí - A
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia. - B
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia. - C
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song. - D
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Câu 7 : Chứng minh định lý là - A
Dùng lập luận để từ giả thiết suy ra kết luận - B
Dùng hình vẽ để từ giả thiết suy ra kết luận - C
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận - D
Câu 8 : Chứng minh định lý là - A
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận. - B
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận - C
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận. - D
Câu 9 : Trong các câu sau, câu nào không cho một định lí: - A
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia - B
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau. - C
Hai góc đối đỉnh thì bằng nhau. - D
Hai góc kề nhau thì có tổng số đo là 180 độ
- A
Định lí thường được phát biểu ở dạng: “ Vì … nên….” - B
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL - C
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ - D
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Lời giải và đáp án - A
Giả thiết của định lý là điều cho biết. - B
Kết luận của định lý là điều được suy ra. - C
Giả thiết của định lý là điều được suy ra. - D
Đáp án : D Phương pháp giải : Sử dụng lý thuyết về định lý. Lời giải chi tiết : Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Câu 2 : Định lý sau được phát biểu thành lời là:  - A
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia. - B
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia. - C
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\) - D
Đáp án : A Phương pháp giải : Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra. Lời giải chi tiết : Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia. Câu 3 : Phát biểu định lý sau bằng lời: 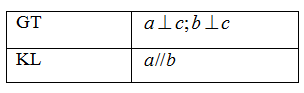 - A
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau. - B
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau. - C
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - D
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Đáp án : C Phương pháp giải : Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết : Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. Câu 4 : Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:  - A
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OF\) - B
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OA\) - C
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\). Kết luận: \(OE \bot OF\) - D
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OB \bot OF\)
Đáp án : A Phương pháp giải : Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết : Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OF\) Câu 5 : Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là  - A
- B
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\) - C
- D
Đáp án : B Phương pháp giải : Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết : Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\) Câu 6 : Trong các câu sau, câu nào cho một định lí - A
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia. - B
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia. - C
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song. - D
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Đáp án : A Phương pháp giải : Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết : Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” Câu 7 : Chứng minh định lý là - A
Dùng lập luận để từ giả thiết suy ra kết luận - B
Dùng hình vẽ để từ giả thiết suy ra kết luận - C
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận - D
Đáp án : A Lời giải chi tiết : Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận. Câu 8 : Chứng minh định lý là - A
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận. - B
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận - C
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận. - D
Đáp án : A Phương pháp giải : Sử dụng định nghĩa “chứng minh định lý”. Lời giải chi tiết : Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận. Câu 9 : Trong các câu sau, câu nào không cho một định lí: - A
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia - B
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau. - C
Hai góc đối đỉnh thì bằng nhau. - D
Hai góc kề nhau thì có tổng số đo là 180 độ
Đáp án : D Phương pháp giải : Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết : + “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” + “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.” + “Hai góc đối đỉnh thì bằng nhau” Câu D không là định lí vì khẳng định D sai - A
Định lí thường được phát biểu ở dạng: “ Vì … nên….” - B
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL - C
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ - D
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Đáp án : A Lời giải chi tiết : Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …” Các khẳng định B,C,D đúng . Luyện tập và củng cố kiến thức Bài 3: Hai đường thẳng song song Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết Luyện tập và củng cố kiến thức Bài 2: Tia phân giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết Luyện tập và củng cố kiến thức Bài 1: Các góc ở vị trí đặc biệt Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
|