Trắc nghiệm Bài tập hay và khó chương 4: Sự tương giao của đường thẳng và parabol Toán 9Làm bài tậpCâu hỏi 1 : Tìm phương trình đường thẳng \(\left( d \right)\) đi qua điểm \(I\left( {0;1} \right)\) và cắt parabol \((P):\) \(y = {x^2}\) tại hai điểm phân biệt \(M\) và \(N\) sao cho \(MN = 2\sqrt {10} \).
Đáp án của giáo viên Xem Lời Giải : B Phương pháp giải : + Viết phương trình đường thẳng \(d\) + Viết phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) + Lập luận dựa vào dữ kiện \(MN = 2\sqrt {10} \) để tìm đường thẳng \(\left( d \right)\) Lời giải chi tiết : Đường thẳng \(\left( d \right)\) qua \(I\) với hệ số góc \(a\) có dạng: \(y = ax + 1\) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là: \({x^2} = ax + 1 \Leftrightarrow {x^2} - ax - 1 = 0\) (1). Vì \(\Delta = {a^2} + 4 > 0\) với mọi \(a\), (1) luôn có hai nghiệm phân biệt nên \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt \(M\left( {{x_1};{y_1}} \right),N\left( {{x_2};{y_2}} \right)\) hay \(M\left( {{x_1};a{x_1} + 1} \right),N\left( {{x_2};a{x_2} + 1} \right)\). Theo định lý Viet ta có: \({x_1} + {x_2} = a,{x_1}{x_2} = - 1\). \(MN = 2\sqrt {10} \)\( \Leftrightarrow {\left( {{x_2} - {x_1}} \right)^2} + {\left( {a{x_2} + 1 - a{x_1} - 1} \right)^2} = 40\)\( \Leftrightarrow \left( {{a^2} + 1} \right){\left( {{x_2} - {x_1}} \right)^2} = 40 \Leftrightarrow \left( {{a^2} + 1} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right] = 40\)\( \Leftrightarrow \left( {{a^2} + 1} \right)\left( {{a^2} + 4} \right) = 40 \)$\Leftrightarrow {a^4} + 5{a^2} - 36 = 0 \Leftrightarrow \left( {{a^2} + 9} \right)\left( {{a^2} - 4} \right) = 0$\(\Rightarrow {a^2} = 4 \Rightarrow a = \pm 2\). Vậy phương trình đường thẳng cần tìm là \(y = 2x + 1;y = - 2x + 1.\) Câu hỏi 2 : Trong mặt phẳng tọa độ \(Oxy\), cho parabol \(\left( P \right)\) có phương trình \(y = \dfrac{{ - {x^2}}}{2}\). Gọi \(\left( d \right)\) là đường thẳng đi qua \(I\left( {0; - 2} \right)\) và có hệ số góc \(k\). Đường thẳng $(d)$ cắt parabol $(P)$ tại hai điểm phân biệt $A, B.$ Gọi \(H,K\) theo thứ tự là hình chiếu vuông góc của \(A,B\) trên trục hoành. Khi đó tam giác \(IHK\) là tam giác
Đáp án của giáo viên Xem Lời Giải : C Phương pháp giải : + Viết phương trình đường thẳng \(\left( d \right)\) + Viết phương trình hoành độ giao điểm + Tính độ dài $IK;IH;HK$ + Sử dụng định lý Pytago đảo để chỉ ra tam giác \(IHK\) vuông. Lời giải chi tiết : Đường thẳng \(\left( d \right):y = kx - 2\) Xét phương trình \(\dfrac{{ - {x^2}}}{2} = kx - 2 \Leftrightarrow {x^2} + 2kx - 4 = 0\) (1). Ta có:\(\Delta ' = {k^2} + 4 > 0\) với mọi \(k\), suy ra (1) có hai nghiệm phân biệt. Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt. Giả sử (1) có hai nghiệm phân biệt \({x_1},{x_2}\) Suy ra \(A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right)\) thì \(H\left( {{x_1};0} \right),K\left( {{x_2};0} \right)\). Khi đó \(I{H^2} = x_1^2 + 4,I{K^2} = x_2^2 + 4,K{H^2} = {\left( {{x_1} - {x_2}} \right)^2}\). Theo định lý Viet thì \({x_1}{x_2} = - 4\) nên \(I{H^2} + I{K^2} = x_1^2 + x_2^2 + 8 = K{H^2}\). Vậy tam giác \(IHK\) vuông tại \(I\). Câu hỏi 3 : Cho Parabol \((P):y = {x^2}\) và đường thẳng \((d):y = mx + 4\) . Biết đường thẳng \((d)\) luôn cắt đồ thị \((P)\) tại hai điểm phân biệt \(A,B\) .Gọi \({x_1},{x_2}\) là hoành độ của các điểm \(A,B.\) Câu 3.1 Tìm giá trị lớn nhất của \(Q = \dfrac{{2\left( {{x_1} + {x_2}} \right) + 7}}{{{x_1}^2 + {x_2}^2}}\) .
Đáp án của giáo viên Xem Lời Giải : C Phương pháp giải : + Viết phương trình hoành độ giao điểm của \(\left( d \right)\) và $\left( P \right)$ + Biến đổi \(Q = \dfrac{{2\left( {{x_1} + {x_2}} \right) + 7}}{{{x_1}^2 + {x_2}^2}}\) để sử dụng được hệ thức Vi-et đưa về biểu thức ẩn \(m\) từ đó lập luận để đánh giá. Lời giải chi tiết : Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là: \({x^2} = mx + 4 \Leftrightarrow {x^2} - mx - 4 = 0\) . Ta có \(\Delta = {m^2} + 16 > 0\), với mọi \(m\) nên phương trình luôn có 2 nghiệm phân biệt, suy ra đường thẳng \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt. Theo định lý Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}.{x_2} = - 4\end{array} \right.\) Ta có $Q = \dfrac{{2\left( {{x_1} + {x_2}} \right) + 7}}{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}}} $\(\Rightarrow Q = \dfrac{{2m + 7}}{{{m^2} + 8}}\). Ta xét \({m^2} + 8 - \left( {2m + 7} \right) = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} \ge 0;\,\,\,\forall m\) nên \({m^2} + 8 \ge 2m + 7 \Rightarrow Q = \dfrac{{2m + 7}}{{{m^2} + 8}} \le 1\) Dấu “=’ xảy ra khi \({m^2} + 8 = 2m + 7 \Leftrightarrow {\left( {m - 1} \right)^2} = 0 \Leftrightarrow m = 1\) Suy ra giá trị lớn nhất của \(Q\) là \(1\) khi \(m = 1.\) Câu 3.2 Tìm \(m\) để diện tích tam giác \(OAB\) bằng \(8\) .
Đáp án của giáo viên Xem Lời Giải : A Phương pháp giải : + Kẻ \(H,K\) lần lượt là hình chiếu vuông góc của điểm \(A,B\) trên trục \(Oy\) + \({S_{OAB}} = {S_{OAI}} + {S_{OBI}} = \dfrac{1}{2}AH.OI + \dfrac{1}{2}BK.OI\) Lời giải chi tiết : 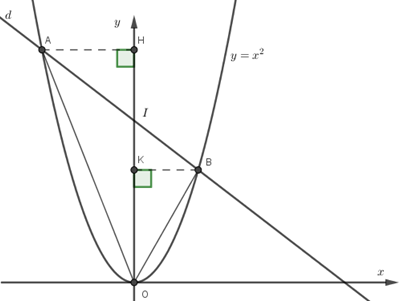 Để ý rằng đường thẳng \(\left( d \right)\) luôn đi qua điểm cố định \(I\left( {0;4} \right)\) nằm trên trục tung. Ngoài ra nếu gọi $A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right)$ thì \({x_1}.{x_2} = - 4 < 0\) (do \({x_1};{x_2}\) là hai nghiệm của phương trình hoành độ giao điểm \({x^2} - mx - 4 = 0\) ) nên hai giao điểm $A,B$ nằm về hai phía trục tung. Giả sử \({x_1} < 0 < {x_2}\) thì ta có: \({S_{OAB}} = {S_{OAI}} + {S_{OBI}} = \dfrac{1}{2}AH.OI + \dfrac{1}{2}BK.OI\) với \(H,K\) lần lượt là hình chiếu vuông góc của điểm \(A,B\) trên trục \(Oy\). Ta có \(OI = 4,AH = \left| {{x_1}} \right| = - {x_1},BK = \left| {{x_2}} \right| = {x_2}\). Suy ra \({S_{OAB}} = 2\left( {{x_2} - {x_1}} \right)\) \( \Rightarrow S_{OAB}^2 = 4{\left( {{x_1} - {x_2}} \right)^2} = 4\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]\). Theo định lý Viet ta có: \({x_1} + {x_2} = m,{x_1}{x_2} = - 4\). Thay vào ta có: $S_{OAB}^2 = 4\left( {{m^2} + 16} \right) = 64 \Leftrightarrow m = 0$. Câu hỏi 4 : Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(\left( d \right):2x - y - {a^2} = 0\) và parabol \(\left( P \right):y = a{x^2}\) \((a > 0)\). Câu 4.1 Tìm \(a\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A,B\). Khi đó có kết luận gì về vị trí của hai điểm \(A,B.\)
Đáp án của giáo viên Xem Lời Giải : A Phương pháp giải : + Sử dụng điều kiện để phương trình bậc hai có hai nghiệm phân biệt \(\left\{ \begin{array}{l}a \ne 0\\\Delta > 0\end{array} \right.\) + Nhận xét tổng và tích của hai nghiệm theo định lý Vi-ét để tìm ra vị trí của hai điểm \(A,B.\) Lời giải chi tiết : Ta có $\left( d \right):2x - y - {a^2} = 0$ $ \Leftrightarrow y = 2x - {a^2}$ Xét phương trình \(a{x^2} = 2x - {a^2}\) \( \Leftrightarrow a{x^2} - 2x + {a^2} = 0\) (1) \(\left( d \right)\) cắt \(\left( P \right)\) .tại hai điểm phân biệt \(A,B\) khi (1) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow a < 1\). Kết hợp với điều kiện $a>0$ ta có \(0 < a < 1\) khi đó (1) có hai nghiệm \({x_A};{x_B}\) ( \({x_A},{x_B}\) là hoành độ của \(A\) và \(B\)) thỏa mãn \(\left\{ \begin{array}{l}{x_A} + {x_B} = \dfrac{2}{a} > 0\\{x_A}.{x_B} = a > 0\end{array} \right.\) (hệ thức Vi-ét) suy ra \({x_A};{x_B}\) dương nên \(A,B\) nằm ở bên phải trục \(Oy\). Câu 4.2 Gọi \({x_A},{x_B}\) là hoành độ của \(A\) và \(B\). Tìm giá trị nhỏ nhất của biểu thức \(T = \dfrac{4}{{{x_A} + {x_B}}} + \dfrac{1}{{{x_A}.{x_B}}}\).
Đáp án của giáo viên Xem Lời Giải : C Phương pháp giải : Sử dụng hệ thức Vi-ét và bất đẳng thức Cô-si Lời giải chi tiết : Theo câu trước ta có \({x_A};{x_B}\) là hai nghiệm của phương trình \(a{x^2} - 2x + {a^2} = 0\) Theo định lý Vi et ta có: \(\left\{ \begin{array}{l}{x_A} + {x_B} = \dfrac{2}{a} > 0\\{x_A}.{x_B} = a > 0\end{array} \right.\). Ta có: \(T = 2a + \dfrac{1}{a}\), với $a>0$ theo bất đẳng thức Cô si cho 2 số dương ta có: \(2a + \dfrac{1}{a} \ge 2\sqrt 2 \). Vậy \(\min T = 2\sqrt 2 \) khi \(a = \dfrac{1}{{\sqrt 2 }}\). Câu hỏi 5 : Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = mx + 1\). Gọi \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) là các giao điểm của \(\left( d \right)\) và \(\left( P \right)\). Tìm \(m\) để biểu thức \(M = \left( {{y_1} - 1} \right)\left( {{y_2} - 1} \right)\) đạt giá trị lớn nhất.
Đáp án của giáo viên Xem Lời Giải : A Phương pháp giải : + Viết phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\). + Đánh giá \(M = \left( {{y_1} - 1} \right)\left( {{y_2} - 1} \right)\) bằng cách sử dụng hệ thức Vi-et. Lời giải chi tiết : Phương trình hoành độ giao điểm của đường thẳng và Parabol là: \({x^2} = mx + 1 \Leftrightarrow {x^2} - mx - 1 = 0\) (1) \(\Delta = {m^2} + 4 > 0\) với mọi \(m\) nên (1) có hai nghiệm phân biệt, suy ra \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) với \({x_1};{x_2}\) là hai nghiệm của phương trình (1). Theo định lý Viet, ta có: \({x_1} + {x_2} = m;{x_1}{x_2} = - 1\) Vì \(A;B \in \left( P \right) \Rightarrow {y_1} = x_1^2;{y_2} = x_2^2\). Ta có $M = \left( {{y_1} - 1} \right)\left( {{y_2} - 1} \right) $$= \left( {x_1^2 - 1} \right)\left( {x_2^2 - 1} \right)$$ = x_1^2x_2^2 - \left( {x_1^2 + x_1^2} \right) + 1$ $ = x_1^2x_2^2 + 2{x_1}{x_2} - {\left( {{x_1} + {x_2}} \right)^2} + 1$ \( = 1 - 2 - {m^2} + 1 = - {m^2} \le 0\) Vậy \(\max M = 0\) khi \(m = 0\). Câu hỏi 6 : Trong mặt phẳng tọa độ \(Oxy\) cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = - \dfrac{2}{3}\left( {m + 1} \right)x + \dfrac{1}{3}\) (\(m\) là tham số). Trong trường hợp \(\left( P \right)\) và \(\left( d \right)\) cắt nhau tại hai điểm phân biệt có hoành độ giao điểm là \({x_1},{x_2}\). Đặt \(f\left( x \right) = {x^3} + \left( {m + 1} \right){x^2} - x\) khi đó
Đáp án của giáo viên Xem Lời Giải : D Phương pháp giải : + Tìm điều kiện của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt. + Sử dụng hệ thức Vi-et và hằng đẳng thức để biến đổi \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\) Lời giải chi tiết : Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) ta có \({x^2} = \dfrac{{ - 2\left( {m + 1} \right)}}{3} + \dfrac{1}{3} \) \(\Leftrightarrow 3{x^2} + 2\left( {m + 1} \right)x - 1 = 10\,\,\,\left( 1 \right)\) Ta thấy phương trình \(\left( 1 \right)\) có hệ số \(a\) và \(c\) trái dấu nên luôn có hai nghiệm phân biệt mọi \(m\) nên \(\left( P \right)\) và \(\left( d \right)\) luôn cắt nhau tại hai điểm phân biệt với mọi \(m\). Theo hệ thức Viet: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - 2\left( {m + 1} \right)}}{3}\\{x_1}{x_2} = \dfrac{{ - 1}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 1 = \dfrac{{ - 3\left( {{x_1} + {x_2}} \right)}}{2}\\3{x_1}{x_2} = - 1\end{array} \right.\) Vì \(f\left( x \right) = {x^3} + \left( {m + 1} \right){x^2} - x\) nên ta có: \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) \)\(= x_1^3 - x_2^3 + \left( {m + 1} \right)\left( {x_1^2 - x_2^2} \right) - {x_1} + {x_2}\) \( \Rightarrow 2\left( {f\left( {{x_1}} \right) - f\left( {{x_2}} \right)} \right) \)\(= 2x_1^3 - 2x_2^3 - 3\left( {{x_1} + {x_2}} \right)\left( {x_1^2 - x_2^2} \right) - 2{x_1} + 2{x_2}\) ( vì \(m + 1 = \dfrac{{ - 3}}{2}\left( {{x_1} + {x_2}} \right)\) ) \( = - x_1^3 + x_2^3 + 3{x_1}{x_2}\left( {{x_2} - {x_1}} \right) - 2\left( {{x_1} - {x_2}} \right) \) \(= - x_1^3 + x_2^3 + \left( {{x_1} - {x_2}} \right) - 2\left( {{x_1} - {x_2}} \right)\) \( = - \left( {x_1^3 - x_2^3 - 3{x_1}{x_2}\left( {{x_1} - {x_2}} \right)} \right) \)\(= \left[ {\left( {{x_1} - {x_2}} \right)\left( {x_1^2 + x_2^2 - 2{x_1}{x_2}} \right)} \right] \)\(= - {\left( {{x_1} - {x_2}} \right)^3}\). Nên \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \dfrac{{ - 1}}{2}{\left( {{x_1} - {x_2}} \right)^3}\) Câu hỏi 7 : Trong mặt phẳng \(Oxy\) cho đường thẳng \(\left( d \right):\,y = kx + \dfrac{1}{2}\) và parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}.\) Giả sử đường thẳng \(\left( d \right)\) cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\). Tọa độ trung điểm \(M\) của đoạn thẳng \(AB\) luôn thỏa mãn phương trình nào dưới đây?
Đáp án của giáo viên Xem Lời Giải : A Phương pháp giải : + Tìm điều kiện của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt. + Sử dụng hệ thức Vi-et và công thức tọa độ trung điểm \(M\) của \(AB:\) \(\left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2}\end{array} \right.\) để biến đổi . Lời giải chi tiết : Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right):\,\,\,\dfrac{1}{2}{x^2} = kx + \dfrac{1}{2}\) \( \Leftrightarrow {x^2} - 2kx - 1 = 0\)\(\left( * \right)\) . Nhận thấy \(a = 1;c = - 1\) trái dấu nhau nên phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt hay đường thẳng \(\left( d \right)\) cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\) với mọi \(k.\) Gọi \(A\left( {{x_A};{y_A}} \right);B\left( {{x_B};{y_B}} \right)\) thì \({x_A};{x_B}\) là hai nghiệm của phương trình \(\left( * \right)\) và \({y_A} = k{x_A} + \dfrac{1}{2};{y_B} = k{x_B} + \dfrac{1}{2}\) Tọa độ trung điểm \(M\) của đoạn \(AB\) là \(\left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{k\left( {{x_A} + {x_B}} \right) + 1}}{2}\end{array} \right.\) Theo hệ thức Vi-ét ta có:\({x_A} + {x_B} = 2k\) nên \(\left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{k\left( {{x_A} + {x_B}} \right) + 1}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = k\\{y_M} = {k^2} + \dfrac{1}{2}\end{array} \right.\) \( \Rightarrow {y_M} = x_M^2 + \dfrac{1}{2}\) Vậy tọa độ điểm \(M\) luôn thỏa mãn phương trình \(y = {x^2} + \dfrac{1}{2}.\) Câu hỏi 8 : Trên parabol \(\left( P \right):y = {x^2}\) ta lấy ba điểm phân biệt \(A\left( {a;{a^2}} \right);B\left( {b;{b^2}} \right);C\left( {c;{c^2}} \right)\) thỏa mãn \({a^2} - b = {b^2} - c = {c^2} - a.\) Hãy tính tích \(T = \left( {a + b + 1} \right)\left( {b + c + 1} \right)\left( {c + a + 1} \right)\)
Đáp án của giáo viên Xem Lời Giải : C Phương pháp giải : + Dựa vào dữ kiện đề bài \({a^2} - b = {b^2} - c = {c^2} - a\) để tính \(a + b + 1;b + c + 1;a + c + 1\) Lời giải chi tiết : Từ đề bài \({a^2} - b = {b^2} - c = {c^2} - a.\) suy ra \({a^2} - {b^2} = b - c\) nên \(a + b = \dfrac{{b - c}}{{a - b}}\)\( \Rightarrow a + b + 1 = \dfrac{{b - c}}{{a - b}} + 1 = \dfrac{{a - c}}{{a - b}}\) Tương tự ta có \(b + c + 1 = \dfrac{{b - a}}{{b - c}};\,c + a + 1 = \dfrac{{c - b}}{{c - a}}\) Vậy \(T = \dfrac{{a - c}}{{a - b}}.\dfrac{{b - a}}{{b - c}}.\dfrac{{c - b}}{{c - a}} = - 1\) Câu hỏi 9 : Cho parabol \(\left( P \right):y = \dfrac{1}{4}{x^2}\) và đường thẳng \(d:y = \dfrac{{11}}{8}x - \dfrac{3}{2}.\) Gọi \(A,B\) là các giao điểm của \(\left( P \right)\) và \(d.\) Tìm tọa độ điểm \(C\) trên trục tung sao cho \(CA + CB\) có giá trị nhỏ nhất.
Đáp án của giáo viên Xem Lời Giải : B Phương pháp giải : Lấy \(A'\) đối xứng với \(A\) qua trục tung, khi đó \(CA + CB = CA' + CB \ge A'B\) Lời giải chi tiết : Hoành độ của \(A\) và \(B\) là nghiệm của phương trình: \(\dfrac{1}{4}{x^2} = \dfrac{{11}}{8}x - \dfrac{3}{2}.\) Phương trình này có hai nghiệm: \(x = 4\) và \(x = \dfrac{3}{2}.\) Suy ra \(A\left( {4;4} \right),B\left( {\dfrac{3}{2};\dfrac{9}{{16}}} \right).\) Dễ thấy hai điểm \(A,B\) cùng nằm về một phía so với trục tung ) (do cùng có hoành độ dương). Lấy điểm \(A'\left( { - 4;4} \right)\) đối xứng với \(A\) qua trục tung. Khi đó \(CA + CB = CA' + CB \ge A'B\), nên \(CA + CB\) đạt giá trị nhỏ nhất khi và chỉ khi \(A',C,B\) thẳng hàng, tức là khi \(C\) là giao điểm của đường thẳng \(A'B\) với trục tung. 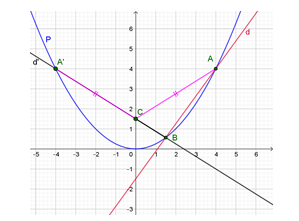 Phương trình đường thẳng \(d'\) đi qua \(A'\) và \(B\) có dạng \(y = ax + b.\) Ta có hệ \(\left\{ \begin{array}{l}4 = - 4a + b\\\dfrac{9}{{16}} = \dfrac{3}{2}a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{5}{8}\\b = \dfrac{3}{2}\end{array} \right..\) Suy ra \(d':y = - \dfrac{5}{8}x + \dfrac{3}{2}.\) Suy ra giao điểm của $(d')$ với trục tung có hoành độ $x=0 \Rightarrow y=\dfrac{3}{2}$ Vậy \(C\left( {0;\dfrac{3}{2}} \right).\) Câu hỏi 10 : Trong mặt phẳng Oxy, cho Parabol \(\left( P \right):y = \dfrac{1}{4}{x^2}\) và đường thẳng \(\left( d \right):x - 2y + 12 = 0\) Gọi giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là \(A,B.\) Tìm tọa độ điểm C nằm trên \(\left( P \right)\) sao cho tam giác $ABC$ vuông tại C.
Đáp án của giáo viên Xem Lời Giải : A Phương pháp giải : + Tìm tọa độ hai điểm \(A;B.\) + Tính $AB;AC;BC$ + Sử dụng định lý Pytago cho tam giác $ABC$ vuông tại \(C:A{C^2} + B{C^2} = A{B^2}\) Lời giải chi tiết : Ta có \(\left( d \right):y = \dfrac{1}{2}x + 6\). Phương trình hoành độ giao điểm \(\dfrac{1}{4}{x^2} = \dfrac{1}{2}x + 6 \Leftrightarrow \left[ \begin{array}{l}x = 6 \Rightarrow y = 9\\x = - 4 \Rightarrow y = 4\end{array} \right.\). Vậy 2 giao điểm \(A\left( {6;9} \right),\,\,B\left( { - 4;4} \right)\). Gọi \(C\left( {c\,\,;\,\,\dfrac{1}{{\,4}}{c^2}} \right) \in \left( P \right)\) \( (c \ne 6,\,\,c \ne - 4)\) là điểm cần tìm. Ta có \(A{B^2} = 125\) ; \(A{C^2} \)\(= {\left( {c - 6} \right)^2} + {\left( {\dfrac{1}{4}{c^2} - 9} \right)^2} \)\(= \dfrac{1}{{16}}{c^4} - \dfrac{7}{2}{c^2} - 12c + 117\) ; \(B{C^2} = {\left( {c + 4} \right)^2} + {\left( {\dfrac{1}{4}{c^2} - 4} \right)^2} \)\(= \dfrac{1}{{16}}{c^4} - {c^2} + 8c + 32\) . Tam giác \(ABC\) vuông tại C khi và chỉ khi \(A{B^2} = A{C^2} + B{C^2}\) \( \Leftrightarrow 125 = \dfrac{1}{{16}}{c^4} - \dfrac{7}{2}{c^2} - 12c + 117 + \dfrac{1}{{16}}{c^4} - {c^2} + 8c + 32\)\( \Leftrightarrow \dfrac{1}{8}{c^4} - \dfrac{9}{2}{c^2} - 4c + 24 = 0 \)\(\Leftrightarrow \dfrac{1}{8}{c^4} - \dfrac{1}{4}{c^3} + \dfrac{1}{4}{c^3} - \dfrac{1}{2}{c^2} - 4{c^2} + 8c - 12c + 24 = 0\)\( \Leftrightarrow \dfrac{1}{8}{c^3}\left( {c - 2} \right) + \dfrac{1}{4}{c^2}\left( {c - 2} \right) - 4\left( {c - 2} \right) - 12\left( {c - 2} \right) = 0\)\( \Leftrightarrow \left( {c - 2} \right)\left( {\dfrac{1}{8}{c^3} + \dfrac{1}{4}{c^2} - 4c - 12} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}c - 2 = 0\\\dfrac{1}{8}{c^3} + \dfrac{1}{4}{c^2} - 4c - 12 = 0\end{array} \right.\) $ \Leftrightarrow \left[ \begin{array}{l} \( \Leftrightarrow \left[ \begin{array}{l}c = 2\,\,\,\,\,\,\left( n \right)\\c = - 4\,\,\,\left( l \right)\\c = 6\,\,\,\,\,\,\left( l \right)\end{array} \right.\) . Vậy \(C\left( {2;1} \right)\) là điểm thỏa đề bài.
|
