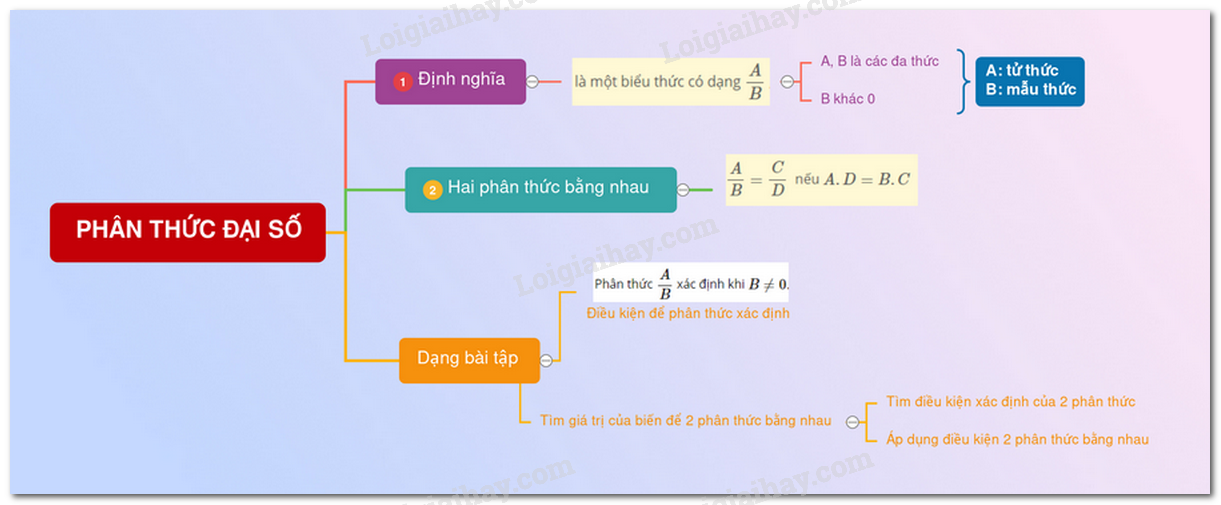
Lý thuyết về phân thức đại số

1. Phân thức đại số

Định nghĩa

Chú ý:  

Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng $1$ .

Ví dụ:

\(\dfrac{x}{{x + 1}}\) là một phân thức đại số. Số \(2\) cũng là một phân thức đại số dưới dạng \(\dfrac{2}{1}.\) 

Hai phân thức bằng nhau

Tính chất cơ bản của phân thức đại số

Quy tắc đổi dấu

Ngoài ra, ta còn có một số quy tắc sau:

+ Đổi dấu tử số và đổi dấu phân thức: $\dfrac{A}{B} = - \dfrac{{ - A}}{B}$ 

+ Đổi dấu mẫu số và đổi dấu phân thức: $\dfrac{A}{B} = - \dfrac{A}{{ - B}}$

+ Đổi dấu mẫu : \(\dfrac{A}{{ - B}} = - \dfrac{A}{B}\)

2. Các dạng toán thường gặp

Dạng 2: Tìm giá trị của biến số \(x\) để phân thức\(\dfrac{A}{B}\) nhận giá trị \(m\) cho trước.

Phương pháp:

Bước 1: Tìm điều kiện để phân thức xác định: \(B \ne 0\)

Bước 2: Từ giả thiết ta có \(\dfrac{A}{B} = m\) . Từ đó tìm được \(x.\)

Bước 3: So sánh với điều kiện ở bước 1 để kết luận.

Dạng 3: Chứng minh hai phân thức bằng nhau. Tìm các giá trị của \(x\) để hai phân thức bằng nhau.

Phương pháp:

Ta sử dụng các kiến thức sau:

+ Với hai phân thức \(\dfrac{A}{B}\) và \(\dfrac{C}{D}\)\(\left( {B \ne 0,\,D \ne 0} \right)\), ta nói \(\dfrac{A}{B} = \dfrac{C}{D}\) nếu $A.D = B.C$

+ \(\dfrac{A}{B} = \dfrac{{A.M}}{{B.M}}\) ($M$ là một đa thức khác $0$ )

+ \(\dfrac{A}{B} = \dfrac{{A:N}}{{B:N}}\) ($N$ là một nhân tử chung, $N$ khác đa thức $0.$)

+ $\dfrac{A}{B} = \dfrac{{ - A}}{{ - B}}.$

3. Bài tập vận dụng

Câu 1. Biểu thức nào sau đây không là phân thức đại số?

A. \(\frac{1}{{\left( {{x^2} + 1} \right)}}\)

B. \(\frac{1}{{\left( {{x^2} + 1} \right)}}\)

C. \({x^2} - 3x + 1\)

D. \(\frac{{{x^2} + 4}}{0}\)

Lời giải

\(\frac{1}{{\left( {{x^2} + 1} \right)}}\) có \(A = 1;\,B = {x^2} + 1 > 0\forall x \Rightarrow \frac{1}{{{x^2} + 1}}\) là phân thức đại số

\(\frac{{x + 3}}{5}\) có \(A = x + 3;\,B = 5 \Rightarrow \frac{{x + 3}}{5}\) là phân thức đại số

\({x^2} - 3x + 1\) có \(A = {x^2} - 3x + 1;\,B = 1 \Rightarrow {x^2} - 3x + 1\) là phân thức đại số

\(\frac{{{x^2} + 4}}{0}\) có \(A = {x^2} + 4;\,B = 0 \Rightarrow \frac{{{x^2} + 4}}{0}\) không là phân thức đại số

Đáp án D

Câu 2. Cặp phân thức nào sau đây bằng nhau?

A. \(\frac{{ - {x^2}y}}{{3xy}}\) và \(\frac{{xy}}{{3y}}\)

B. \(\frac{{ - {x^2}y}}{{xy}}\) và \(\frac{{3y}}{{xy}}\)

C. \(\frac{3}{{24x}}\) và \(\frac{{2y}}{{16xy}}\)

D. \(\frac{{3xy}}{5}\) và \(\frac{{3{x^2}y}}{{5y}}\)

Lời giải

Ta có: \(\frac{{ - {x^2}y}}{{3xy}} = \frac{{ - x}}{3};\,\frac{{xy}}{{3y}} = \frac{x}{3}\)
Vì \(\frac{{ - x}}{3} \ne \frac{x}{3} \) nên \( \frac{{ - {x^2}y}}{{3xy}} \ne \frac{{xy}}{{3y}}\)
Ta có: \(\frac{{ - {x^2}y}}{{xy}} = - x;\,\frac{{3y}}{{xy}} = \frac{3}{x}\)
Vì \( - x \ne \frac{3}{x} \) nên \( \frac{{ - {x^2}y}}{{xy}} \ne \frac{{3y}}{{xy}}\)
Ta có: \(\frac{3}{{24x}} = \frac{1}{{8x}};\,\frac{{2y}}{{16xy}} = \frac{1}{{8x}} \)
Suy ra \( \frac{3}{{24x}} = \frac{{2y}}{{16xy}}\)
Vì \(\frac{{3{x^2}y}}{{5y}} = \frac{{3{x^2}}}{5} \ne \frac{{3xy}}{5} \) nên \( \frac{{3xy}}{5} \ne \frac{{3{x^2}y}}{{5y}}\)

Đáp án C

Câu 3. Với điều kiện nào của \(x\) thì phân thức \(\frac{{5{\rm{x}} - 7}}{{{x^2} - 9}}\) có nghĩa?

A. \(x \ne 3\)

B. \(x \ne \frac{7}{5}\)

C. \(x \ne - 3\)

D. \(x \ne \pm 3\)

Lời giải

Phân thức \(\frac{{5{\rm{x}} - 7}}{{{x^2} - 9}}\) có nghĩa khi \({x^2} - 9 \ne 0 \) hay \( x \ne \pm 3\)

Đáp án D

Câu 4. Phân thức \(\frac{{7x + 2}}{{5 - 3x}}\) có giá trị bằng \(\frac{{11}}{7}\) khi \(x\) bằng:

A. 1

B. \(\frac{1}{2}\)

C. 2

D. Không có giá trị \(x\) thỏa mãn

Lời giải

Điều kiện: \(5 - 3x \ne 0 \Leftrightarrow x \ne \frac{5}{3}\)

Để \(\frac{{7x + 2}}{{5 - 3x}} = \frac{{11}}{7} \Leftrightarrow \left( {7x + 2} \right)7 = 11\left( {5 - 3x} \right) \Leftrightarrow 49x + 14 = 55 - 33x\)

\( \Leftrightarrow 82x = 41 \Leftrightarrow x = \frac{1}{2}\) (thỏa mãn điều kiện)

Đáp án B

Câu 5. Tìm \(a\) để \(\frac{{a{x^4}{y^4}}}{{ - 4x{y^2}}} = \frac{{{x^3}{y^3}}}{{4y}}\):

A. \(a = - 2x\)

B. \(a = - x\)

C. \(a = - y\)

D. \(a = - 1\)

Lời giải

Ta có: \(a{x^4}{y^4}.4y = 4a{x^4}{y^5}\) và \( - 4x{y^2}.{x^3}{y^3} = - 4{x^4}{y^5}\)

Để \(\frac{{a{x^4}{y^4}}}{{ - 4x{y^2}}} = \frac{{{x^3}{y^3}}}{{4y}}\)thì \(4a{x^4}{y^5} = - 4{x^4}{y^5}\).

Do đó \(4a = - 4\) nên \(a = - 1\)

Đáp án D

Câu 6. Hãy tìm phân thức \(\frac{P}{Q}\) thỏa mãn đẳng thức: \(\frac{{\left( {5x + 3} \right)P}}{{5x - 3}} = \frac{{\left( {2x - 1} \right)Q}}{{25{x^2} - 9}}\)

A. \(\frac{P}{Q} = \frac{{{{\left( {2x - 1} \right)}^2}}}{{5x + 3}}\)

B. \(\frac{P}{Q} = \frac{{{{\left( {2x - 1} \right)}^2}}}{{{{\left( {5x + 3} \right)}^2}}}\)

C. \(\frac{P}{Q} = \frac{{2x - 1}}{{{{\left( {5x + 3} \right)}^2}}}\)

D. \(\frac{P}{Q} = \frac{{2x - 1}}{{{{\left( {5x - 3} \right)}^2}}}\)

Lời giải

\(\frac{{\left( {5x + 3} \right)P}}{{5x - 3}} = \frac{{\left( {2x - 1} \right)Q}}{{25{x^2} - 9}} \\ \frac{{\left( {5x + 3} \right)P}}{{5x - 3}} = \frac{{\left( {2x - 1} \right)Q}}{{\left( {5x + 3} \right)\left( {5x - 3} \right)}}\)

Suy ra \(\left( {5x + 3} \right)P\left( {5x + 3} \right)\left( {5x - 3} \right) = \left( {2x - 1} \right)Q\left( {5x - 3} \right)\)

\( {\left( {5x + 3} \right)^2}P = \left( {2x - 1} \right)Q\\ \frac{P}{Q} = \frac{{2x - 1}}{{{{\left( {5x + 3} \right)}^2}}}\)

Đáp án C

Câu 7. Điều kiện để phân thức \(\frac{{2x - 5}}{3} < 0\) là?

A. \(x > \frac{5}{2}\)

B. \(x < \frac{5}{2}\)

C. \(x < - \frac{5}{2}\)

D. \(x > 5\)

Lời giải

Để \(\frac{{2x - 5}}{3} < 0\) thì \(2x - 5 < 0\)

Suy ra \(2x < 5\)

Do đó \(x < \frac{5}{2}\)

Đáp án B

Câu 8. Đưa phân thức \(\frac{{\frac{1}{3}x - 2}}{{{x^2} - \frac{4}{3}}}\) về phân thức có tử và mẫu là các đa thức với hệ số nguyên.

A. \(\frac{{x - 6}}{{3{x^2} - 4}}\)

B. \(\frac{{x - 2}}{{3{x^2} - 4}}\)

C. \(\frac{{x - 6}}{{{x^2} - 4}}\)

D. \(\frac{{3x - 2}}{{3{x^2} - 4}}\)

Lời giải

Ta có: \(\frac{{\frac{1}{3}x - 2}}{{{x^2} - \frac{4}{3}}} = \frac{{3\left( {\frac{1}{3}x - 2} \right)}}{{3\left( {{x^2} - \frac{4}{3}} \right)}} = \frac{{x - 6}}{{3{x^2} - 4}}\)

Đáp án A

Câu 9. Tìm giá trị lớn nhất của phân thức \(A = \frac{{16}}{{{x^2} - 2x + 5}}\)

A. 2

B. 4

C. 8

D. 16

Lời giải

Ta có: \({x^2} - 2x + 5 = {x^2} - 2x + 1 + 4 = {\left( {x - 1} \right)^2} + 4\)

Vì \({\left( {x - 1} \right)^2} \ge 0\forall x\) nên \({\left( {x - 1} \right)^2} + 4 \ge 4\forall x\) hay \({x^2} - 2x + 5 \ge 4\)

\( \Rightarrow \frac{{16}}{{{x^2} - 2x + 5}} \le \frac{{16}}{4} \Leftrightarrow A \le 4\)

Dấu “=” xảy ra \( \Leftrightarrow {\left( {x - 1} \right)^2} = 0 \Leftrightarrow x = 1\)

Vậy với \(x = 1\) thì \(A\) đạt giá trị lớn nhất là 4.

Đáp án B

Câu 10. Cho \(4{a^2} + {b^2} = 5ab\) và \(2a > b > 0\). Tính giá trị của biểu thức \(A = \frac{{ab}}{{4{a^2} - {b^2}}}\).

A. \(\frac{1}{9}\)

B. \(\frac{1}{3}\)

C. 3

D. 9

Lời giải

Ta có: \(4{a^2} + {b^2} = 5ab \Leftrightarrow 4{a^2} - 5ab + {b^2} = 0 \Leftrightarrow 4{a^2} - 4ab - ab + {b^2} = 0\)

\( \Leftrightarrow 4a\left( {a - b} \right) - b\left( {a - b} \right) = 0 \Leftrightarrow \left( {4a - b} \right)\left( {a - b} \right) = 0\)

Do \(2a > b > 0 \Rightarrow 4a > b \Rightarrow 4a - b > 0\)

\( \Rightarrow a - b = 0 \Leftrightarrow a = b\)

Vậy \(A = \frac{{ab}}{{4{a^2} - {b^2}}} = \frac{{a.a}}{{4{a^2} - {a^2}}} = \frac{{{a^2}}}{{3{a^2}}} = \frac{1}{3}\)

Đáp án B