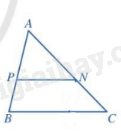
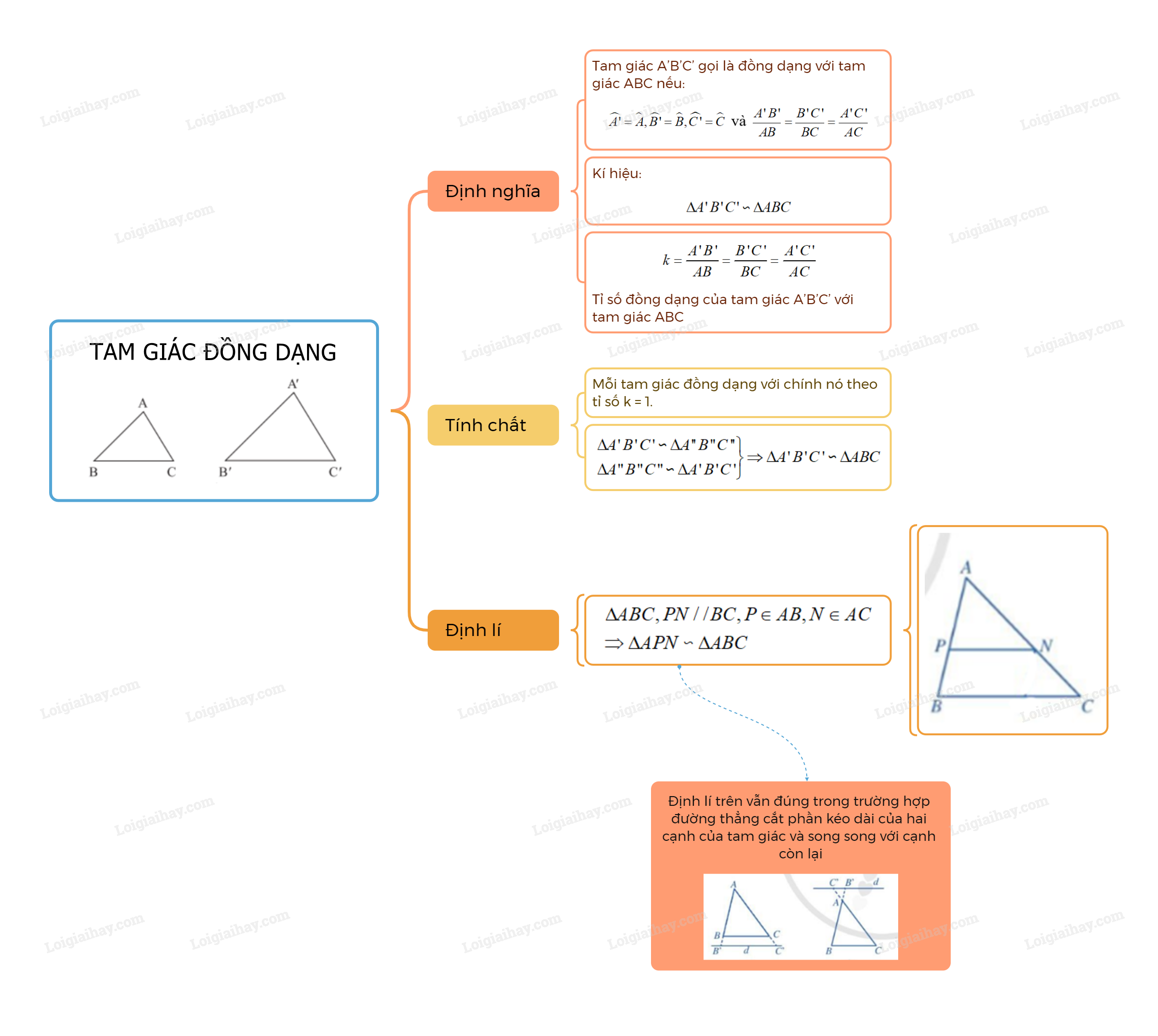
Lý thuyết Tam giác đồng dạng SGK Toán 8 - Cánh diềuTam giác đồng dạng là gì? Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên 1. Tam giác đồng dạng Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu: \(\widehat {A'} = \widehat A,\widehat {B'} = \widehat B,\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) Kí hiệu: \(\Delta A'B'C' \backsim \Delta ABC\) (viết theo thứ tự cặp đỉnh tương ứng). Tỉ số \(k = \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) là tỉ số đồng dạng của \(\Delta A'B'C'\) với \(\Delta ABC\). Nếu \(\Delta A'B'C' = \Delta ABC\) thì \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số đồng dạng là 1. 2. Tính chất Tính chất 1. Mỗi tam giác đồng dạng với chính nó. Tính chất 2. Nếu tam giác \(\Delta A''B''C'' \backsim \Delta A'B'C'\) và \(\Delta A'B'C' \backsim \Delta ABC\) thì \(\Delta A''B''C'' \backsim \Delta ABC\). 3. Định lí Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. \(\begin{array}{l}\Delta ABC,PN//BC,P \in AB,N \in AC\\ \Rightarrow \Delta APN \backsim \Delta ABC\end{array}\)
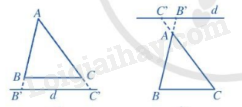
Chú ý: Định lí trên cũng đúng trong trường hợp đường thẳng cắt phần kéo dài của hai cạnh của tam giác và song song với cạnh còn lại.
|