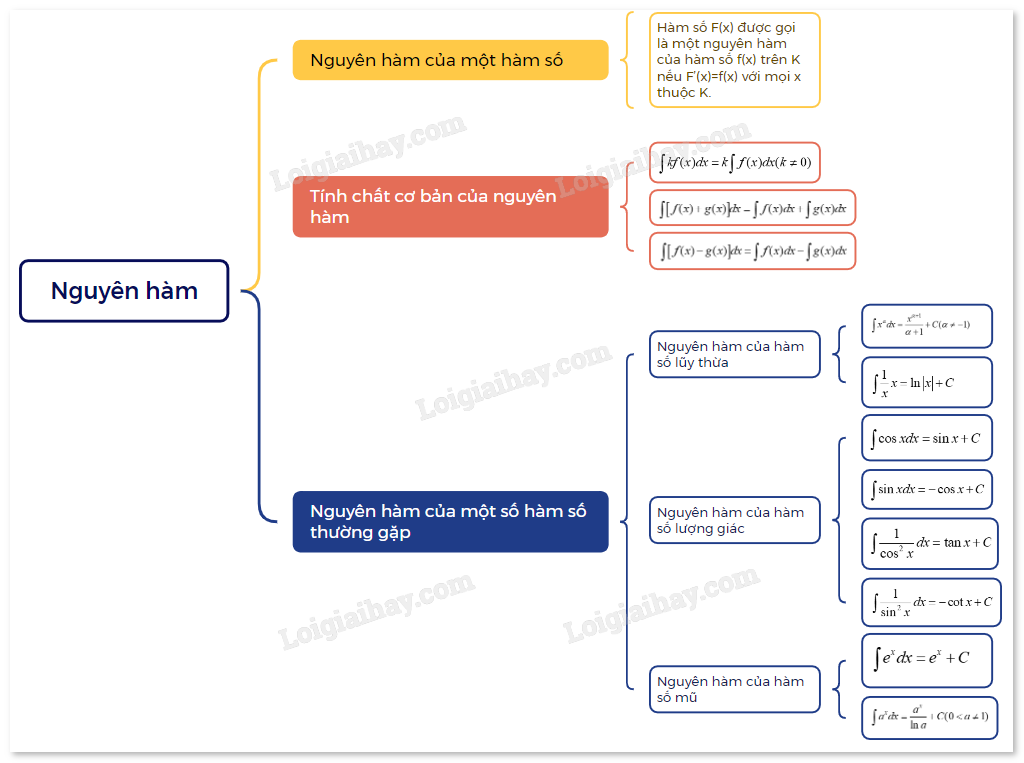
Lý thuyết Nguyên hàm Toán 12 Cùng khám phá

1. Khái niệm nguyên hàm

Chú ý:

Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:

a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K.

b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K.

Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + với C thuộc R là họ các nguyên hàm của f(x) trên K, kí hiệu $\int {f(x)dx} = F(x) + C$.

Ví dụ: Chứng minh $\int {kdx} = kx + C$ với k là hằng số khác 0.

Giải:

Ta có $(kx)' = k$ nên $F(x) = kx$ là một nguyên hàm của hàm số $f(x) = k$.

Vậy $\int {kdx} = kx + C$.

Nhận xét:

Ta có $\int {0dx} = C$, $\int {dx} = \int {1dx} = x + C$.

2. Nguyên hàm của một số hàm số thường gặp

Nguyên hàm của hàm số lũy thừa

Ví dụ:

a) $\int {{x^5}dx} = \frac{1}{6}{x^6} + C$.

b) $\int {{x^{\sqrt 2 }}dx} = \frac{1}{{\sqrt 2 + 1}}{x^{\sqrt 2 + 1}} + C$.

c) $\int {{x^{ - 1}}dx} = \int {\frac{1}{x}dx = } \ln \left| x \right| + C$.

Nguyên hàm của hàm số mũ

Ví dụ:

a) $\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C$.

b) $\int {{e^{3x}}dx} = \int {{{\left( {{e^3}} \right)}^x}dx} = \frac{{{{\left( {{e^3}} \right)}^x}}}{{\ln {e^3}}} + C = \frac{1}{3}{e^{3x}} + C$.

c) $\int {{2^x}{{.3}^x}dx} = \int {{6^x}dx} = \frac{{{6^x}}}{{\ln 6}} + C$.

Nguyên hàm của hàm số lượng giác

Ví dụ:

a) $\int {(1 + {{\tan }^2}x)dx} = \int {\frac{1}{{{{\cos }^2}x}}dx} = \tan x + C$.

b) Tìm nguyên hàm F(x) của hàm số f(x) = sinx, biết $F(2\pi ) = 0$.

Ta có $\int {\sin xdx} = - \cos x + C$.

F(x) là nguyên hàm của hàm số f(x) = sinx nên có dạng F(x) = -cosx + C.

Vì $F(2\pi ) = 0$ nên $- \cos 2\pi + C = 0$ hay $- 1 + C = 0$, suy ra C = 1.

Vậy F(x) = 1 – cosx.

3. Tính chất cơ bản của nguyên hàm

Ví dụ:

a) $\int {6{x^3}dx} = 6\int {{x^3}dx} = 6.\frac{{{x^4}}}{4} + C = \frac{3}{2}{x^4} + C$.

b) $\int {(3{x^2} - \cos x)dx} = 3\int {{x^2}dx} - \int {\cos xdx} = {x^3} - \sin x + C$.

c) $\int {\left( {\frac{2}{{{{\cos }^2}x}} - {5^x}} \right)dx} = 2\int {\frac{1}{{{{\cos }^2}x}}dx} - \int {{5^x}dx} = 2\tan x - \frac{{{5^x}}}{{\ln 5}} + C$.