Lý thuyết Căn bậc hai của một số thực không âm Toán 9 Cùng khám phá1. Khái niệm về căn bậc hai của số thực không âm Định nghĩa căn bậc hai Căn bậc hai của một số thực a không âm là số x sao cho . Lưu ý: 1. Khái niệm về căn bậc hai của số thực không âm Định nghĩa căn bậc hai
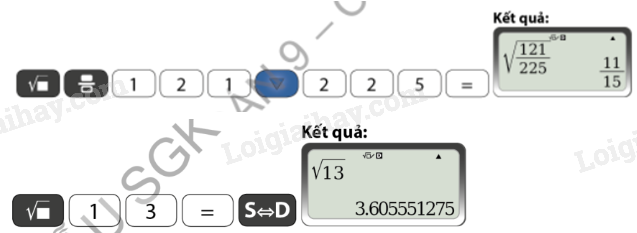
Lưu ý: - Số dương a có đúng hai căn bậc hai là hai số đối nhau, trong đó số dương là √a và số âm là −√a. - Số 0 có đúng một căn bậc hai là chính nó, ta viết √0=0. - Với hai số a và b không âm, nếu a<b thì √a<√b. Ví dụ: +) √81=9 nên 81 có hai căn bậc hai là 9 và -9. +) Căn bậc hai số học của 121 là √121=11. 2. Tính giá trị (đúng hoặc gần đúng) căn bậc hai của một số hữu tỉ bằng máy tính cầm tay
Ví dụ:
3. Căn bậc hai của một bình phương
Ví dụ: √(1+√2)2=|1+√2|=1+√2; √(−3)2=|−3|=3. 4. Căn bậc hai của một tích
Ví dụ: √81.49=√81.√49=9.7=63; √1,3.√10.√13=√1,3.10.13=√13.13=√132=13. Lưu ý: Tính chất trên có thể mở rộng cho tích của nhiều số không âm. Chẳng hạn với a, b, c là ba số không âm, ta có √abc=√a.√b.√c. 5. Căn bậc hai của một thương
Ví dụ: √425=√4√25=25; √216√6=√2166=√36=6. Đưa thừa số ra ngoài dấu căn
Ví dụ: √72.2=7√2; √(−11)2.3=|−11|.√3=11√3. Đưa thừa số vào trong dấu căn
Ví dụ: 2√12=√22.12=√2; 4√74−√28=√42.74−√28=√4.7−√28=√28−√28=0. 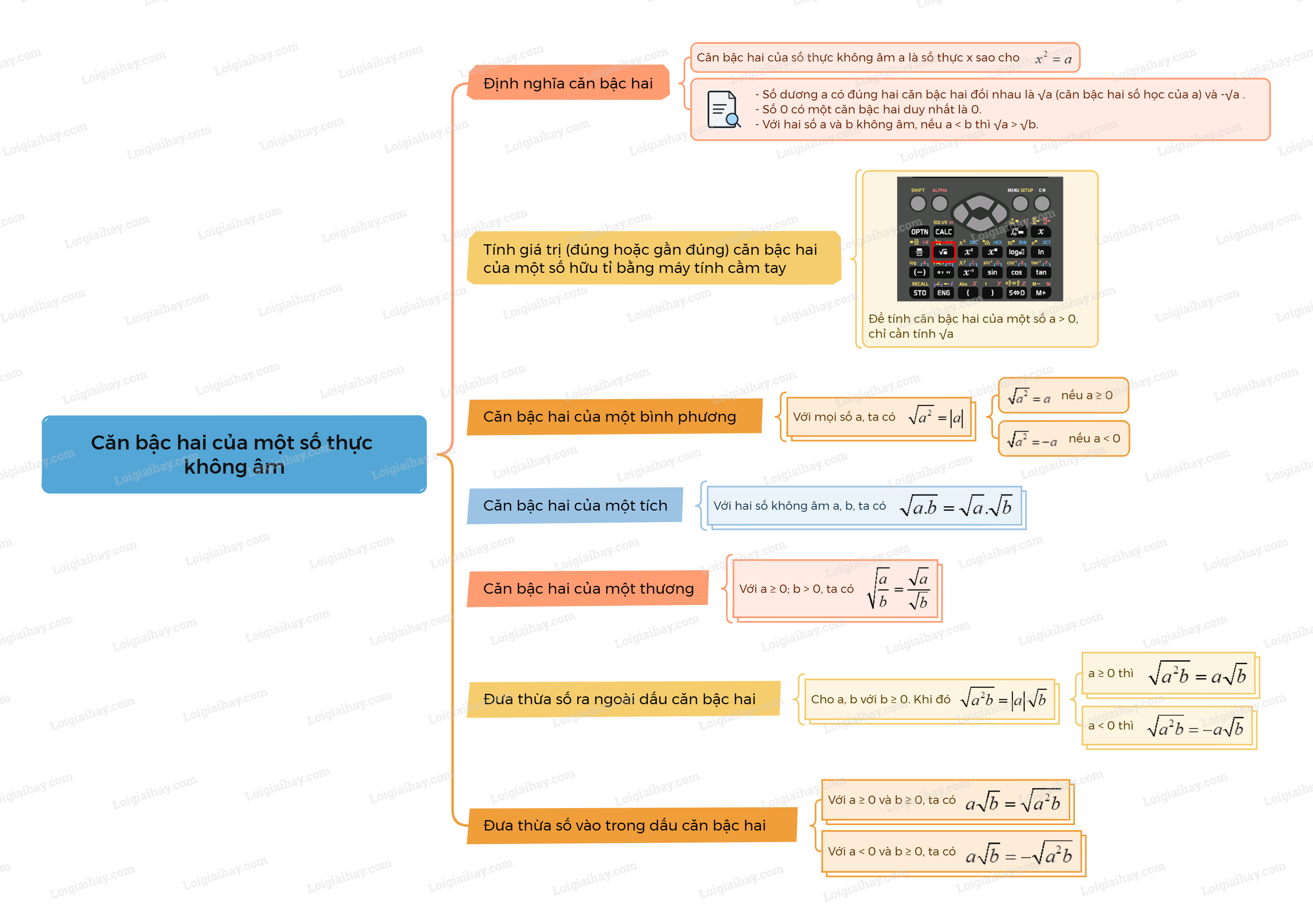
|