Bài tập chủ đề 6 trang 117 Vật Lí 10 Cánh diều

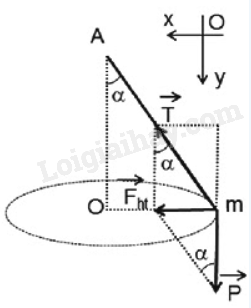
Phương pháp giải:

+ Mối liên hệ giữa tốc độ góc và chu kì là: \(\omega = \frac{{2\pi }}{T}\)

Trong đó: \(\omega \)là tốc độ góc (rad/s); T là chu kì (s)

+ Mối liên hệ giữa tốc độ góc, tốc độ và khoảng cách từ tâm Trái Đất đến vị trí vật: \(v = \omega .R\)

Trong đó: v là tốc độ của vật (m/s); R là khoảng cách từ tâm Trái Đất đến vị trí vật (m)

Lời giải chi tiết:

Ta có: T = 24 giờ = 24.3600 = 86400 s; R = 6400 km = 6,4.10⁶ m

Tốc độ góc của tàu thủy là: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{86400}} \approx {7.10^{ - 5}}(rad/s)\)

Tốc độ của tàu thủy là: \(v = \omega .R = {7.10^{ - 5}}.6,{4.10^6} = 448(m/s)\)

Phương pháp giải:

+ Mối liên hệ giữa tốc độ góc và chu kì là: \(\omega = \frac{{2\pi }}{T}\)

Trong đó: \(\omega \)là tốc độ góc (rad/s); T là chu kì (s)

+ Mối liên hệ giữa tốc độ góc, tốc độ và khoảng cách từ tâm Trái Đất đến vị trí vật: \(v = \omega .R\)

Trong đó: v là tốc độ của vật (m/s); R là khoảng cách từ tâm Trái Đất đến vị trí vật (m)

+ Biểu thức tính gia tốc hướng tâm: \({a_{ht}} = {\omega ^2}.R = \frac{{{v^2}}}{R}\)

+ Biểu thức tính lực hướng tâm: \({F_{ht}} = m.{a_{ht}}\)

Lời giải chi tiết:

Ta có: 867 ngày = 867.86400 s; R = 2,3.10¹¹ m; m = 6,4.10²³ kg.

a) Tốc độ trên quỹ đạo của Hỏa Tính là: \(v = \omega .R = \frac{{2\pi }}{T}.R = \frac{{2\pi }}{{687.86400}}.2,{3.10^{11}} \approx 24346,54(m/s)\)

b) Gia tốc hướng tâm của Hỏa Tinh là:

\({a_{ht}} = \frac{{{v^2}}}{R} = \frac{{24346,{{54}^2}}}{{2,{{3.10}^{11}}}} \approx 5,{6.10^{ - 3}}(m/{s^2})\)

c) Lực hấp dẫn mà Mặt Trời tác dụng lên Hỏa Tinh chính là lực hướng tâm của Hỏa Tinh

=> \({F_{ht}} = m.{a_{ht}} = 6,{4.10^{23}}.2,{6.10^{ - 3}} = 16,{64.10^{20}}(N)\)

Vậy lực hấp dẫn mà Mặt Trời tác dụng Hỏa Tinh là 16,64.10²⁰ N.

 Lời giải chi tiết:

Chọn hệ quy chiếu như hình vẽ

Theo định luật II Newton ta có: \(\overrightarrow P + \overrightarrow T = \overrightarrow {{F_{ht}}} \) (1)

Từ hình vẽ ta có: R = l.sinα

Chiếu (1) lên trục Ox có:

\(\begin{array}{l}T.\sin \alpha = {F_{ht}}\\ \Leftrightarrow T.\sin \alpha = m.\frac{{{v^2}}}{R} \Leftrightarrow {v^2} = \frac{{T.\sin \alpha .R}}{m}\\ \Leftrightarrow {v^2} = \frac{{T.l.{{\sin }^2}\alpha }}{m} \Rightarrow {v_{\max }} \Leftrightarrow {T_{\max }},\sin \alpha = 1\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.l}}{m}} = \sqrt {\frac{{0,8.0,3}}{{0,2}}} \approx 1,1(m/s)\end{array}\)

Lời giải chi tiết:

Khi vật chuyển động trên đường tròn quỹ đạo thì:

+ Tốc độ có độ lớn không đổi, chiều của vận tốc thay đổi

+ Động năng có độ lớn không đổi

+ Động lượng có độ lớn không đổi, chiều thay đổi

+ Lực hướng tâm có độ lớn và chiều không đổi

+ Gia tốc hướng tâm có chiều và độ lớn không đổi.

Phương pháp giải:

Biểu thức tính lực đàn hồi: \({F_{dh}} = K.\left| {\Delta l} \right|\)

Trong đó K là độ cứng của lò xo (N/m); Δl là độ dãn (độ nén) của lò xo (m)

Lời giải chi tiết:

Ta có: K = 25 N/m; Δl = 4 cm = 0,04 m.

Khi cân bằng ta có

\(\begin{array}{l}P = {F_{dh}} \Leftrightarrow mg = K.\left| {\Delta l} \right|\\ \Rightarrow m = \frac{{K.\left| {\Delta l} \right|}}{g} = \frac{{25.0,04}}{{9,8}} \approx 0,1(kg)\end{array}\)