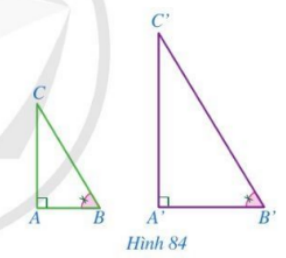
Giải mục 2 trang 84 SGK Toán 8 – Cánh diềuCho hai tam giác ABC và A’B’C’ có Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên Lựa chọn câu để xem lời giải nhanh hơn HĐ2 Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\widehat {B'} = \widehat B\) (Hình 84). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).
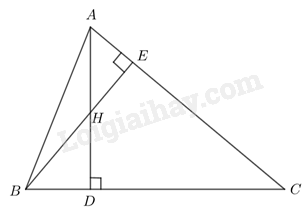
Phương pháp giải: Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba. Lời giải chi tiết: Xét tam giác A’B’C’ và tam giác ABC có: \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) \( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (g-g) LT2 Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh \(HA.HD = HB.HE\). Phương pháp giải: - Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác EHA và DHB đồng dạng. - Suy ra tỉ số đồng dạng tương ứng. Lời giải chi tiết:
Xét tam giác EHA và tam giác DHB có: \(\widehat {EHA} = \widehat {DHB}\) (đối đỉnh) \(\widehat {AEH} = \widehat {BDH} = 90^\circ \) \( \Rightarrow \Delta EHA \backsim \Delta DHB\) (g-g) \( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}}\) (Tỉ số đồng dạng) \( \Rightarrow HA.HD = HB.HE\)
|