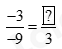Giải mục 2 trang 31, 32, 33, 34 SGK Toán 8 tập 1 - Cánh diều

HĐ3

a) Tính số thích hợp vào ?: ; 

b) Hãy nhắc lại tính chất cơ bản của phân số.

Phương pháp giải:

Vận dụng quy tắc để hai phân số bằng nhau.

Lời giải chi tiết:

b) Tính chất cơ bản của phân số như sau:

- Nếu nhân cả tử và mẫu của một phân số với cùng một số tự nhiên khác 0 thì được một phân số mới bằng phân số đã cho:

\(\dfrac{a}{b} = \dfrac{{a.c}}{{b.c}}\left( {c \ne 0} \right)\)

- Nếu chia cả tử và mẫu của một phân số cho cùng một số tự nhiên khác 0 thì ta cũng được phân số mới bằng phân số đã cho.

\(\dfrac{a}{b} = \dfrac{{a:d}}{{b:d}}\left( {d \ne 0} \right)\)

LT3

Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: \(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\)

Phương pháp giải:

Vận dụng các tính chất cơ bản của phân thức đại số để giải thích

Lời giải chi tiết:

\(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{\left( {3{\rm{x}} + y} \right).y}}{{y.y}} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\) (y là đa thức khác đa thức 0)

HĐ4

Cho phân thức: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}}\)

a) Tìm nhân tử chung của tử và mẫu

b) Tìm phân thức nhận được sau khi chia cả tử và mẫu cho nhân tử chung đó.

Phương pháp giải:

Dùng phương pháp phân tích các đơn thức thành tích của các thừa số để tìm nhân tử chung.

Lời giải chi tiết:

a) Ta có: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{2{\rm{x}}.2{\rm{x}}y}}{{3y.2{\rm{x}}y}}\)

Nhân tử chung của cả tử và mẫu là: 2xy

b) Chia cả tử và mẫu của phân thức đã cho cho nhân tử chung 2xy ta được:

\(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{\left( {4{{\rm{x}}^2}y} \right):2{\rm{x}}y}}{{\left( {6{\rm{x}}{y^2}} \right):2{\rm{x}}y}} = \dfrac{{2{\rm{x}}}}{{3y}}\)

LT4

Rút gọn mỗi phân thức sau:

\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}}\) \(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}}\)

Phương pháp giải:

Bước 1: Phân tử và mẫu thành nhân tử (nếu cần)

Bước 2: Tìm nhân tử chung của cả tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.

Lời giải chi tiết:

\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}} = \dfrac{{4{\rm{x}}.\left( {2{\rm{x}} + 1} \right)}}{{\left( {1 - 2{\rm{x}}} \right).\left( {1 + 2{\rm{x}}} \right)}} = \dfrac{{4{\rm{x}}}}{{1 - 2{\rm{x}}}}\)

\(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}} = \dfrac{{x\left( {{x^2} - {y^2}} \right)}}{{2{\rm{x}}\left( {x + y} \right)}} = \dfrac{{x\left( {x + y} \right)\left( {x - y} \right)}}{{2{\rm{x}}\left( {x + y} \right)}} = \dfrac{{x - y}}{2}\)

HĐ5

Cho hai phân thức \(\dfrac{1}{{{x^2}y}}\) và \(\dfrac{1}{{x{y^2}}}\)

a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.

b) Nhân xét gì về mẫu của hai phân thức thu được.

Phương pháp giải:

Thực hiện theo tính chất cơ bản của phân thức.

Lời giải chi tiết:

a) Ta có:

\(\dfrac{1}{{{x^2}y}} = \dfrac{{1.y}}{{{x^2}y.y}} = \dfrac{y}{{{x^2}{y^2}}}\)

\(\dfrac{1}{{x{y^2}}} = \dfrac{{1.x}}{{x{y^2}.x}} = \dfrac{x}{{{x^2}{y^2}}}\)

b) Mẫu của hai phân thức thu được giống nhau đều là: \({x^2}{y^2}\)

LT5

Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:

a) \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\)

b) \(\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}}\) và \(\dfrac{2}{{{x^2} - 25}}\)

Phương pháp giải:

Bước 1: Phân tích mẫu của mỗi phân thức rồi tìm MTC.

Bước 2: Tìm nhân tử phụ của mỗi phân thức (Bằng cách chia MTC cho từng mẫu)

Bước 3: Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng.

Lời giải chi tiết:

a) MTC chọn là: \(2{{\rm{x}}^2}{y^4}\)

Nhân tử phụ của \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\) lầm lượt là: y; 2x

Vậy: \(\begin{array}{l}\dfrac{5}{{2{{\rm{x}}^2}{y^3}}} = \dfrac{{5.y}}{{2{{\rm{x}}^2}{y^3}.y}} = \dfrac{{5y}}{{2{{\rm{x}}^2}{y^4}}}\\\dfrac{3}{{x{y^4}}} = \dfrac{{3.2{\rm{x}}}}{{x{y^4}.2{\rm{x}}}} = \dfrac{{6{\rm{x}}}}{{2{{\rm{x}}^2}{y^4}}}\end{array}\)

b) Ta có:

\(\begin{array}{l}\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}} = \dfrac{3}{{2{\rm{x}}\left( {x - 5} \right)}}\\\dfrac{2}{{{x^2} - 25}} = \dfrac{2}{{\left( {x - 5} \right)\left( {x + 5} \right)}}\end{array}\)

Chọn MTC là: \(2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)\)

Nhân tử phụ của các mẫu thức trên lần lượt là: \(\left( {x + 5} \right);2{\rm{x}}\)

Vậy:

\(\begin{array}{l}\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}} = \dfrac{3}{{2{\rm{x}}\left( {x - 5} \right)}} = \dfrac{{3\left( {x + 5} \right)}}{{2{\rm{x}}.\left( {x - 5} \right)\left( {x + 5} \right)}}\\\dfrac{2}{{{x^2} - 25}} = \dfrac{2}{{\left( {x - 5} \right)\left( {x + 5} \right)}} = \dfrac{{2.2{\rm{x}}}}{{2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)}} = \dfrac{{4{\rm{x}}}}{{2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)}}\end{array}\)
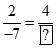