Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh diều

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 16 SGK Toán 12 Cánh diều

Cho hàm số $f\left( x \right) = x + \frac{1}{{x - 1}}$ với $x > 1$.

a) Tính $\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$.

b) Lập bảng biến thiên của hàm số $f\left( x \right)$ trên khoảng $\left( {1; + \infty } \right)$.

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $f\left( x \right)$ trên khoảng $\left( {1; + \infty } \right)$.

Phương pháp giải:

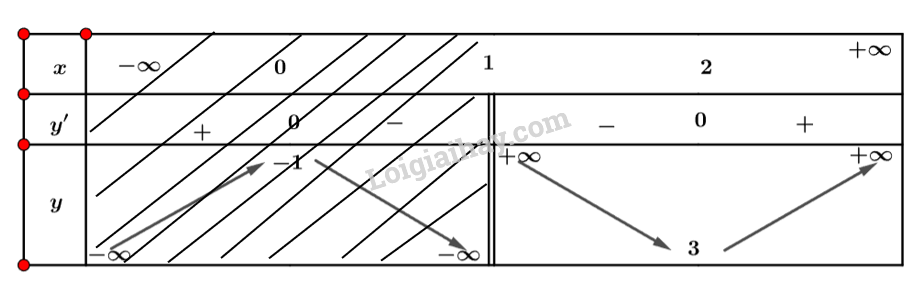
a) Ta có: $\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.$

b) Bảng biến thiên của hàm số trên khoảng $\left( {1; + \infty } \right)$ là:

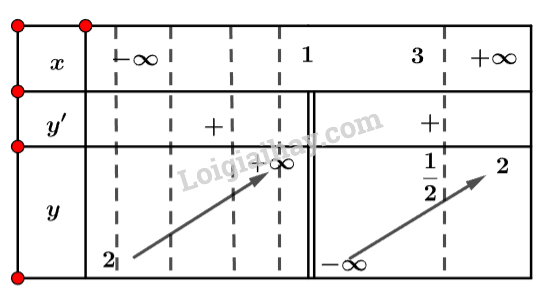
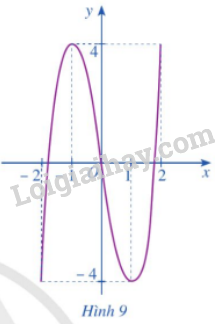
c) Hàm số có giá trị nhỏ nhất bằng 3 khi $x = 2$ và không có giá trị lớn nhất.

Lời giải chi tiết:

a) Ta có: $\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.$

b) Bảng biến thiên của hàm số trên khoảng $\left( {1; + \infty } \right)$ là:

c) Hàm số có giá trị nhỏ nhất bằng 3 khi $x = 2$ và không có giá trị lớn nhất.

LT2

Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y = \frac{{2x - 5}}{{x - 1}}$ trên nửa khoảng $(1;3]$.

Phương pháp giải:

B1: Tìm tập xác định của hàm số.

B2: Tính $y'$. Tìm các điểm mà tại đó $y' = 0$ hoặc $y'$ không tồn tại.

B3: Lập bảng biến thiên của hàm số.

B4: Dựa vào bảng biến thiên để kết luận.

Lời giải chi tiết:

Ta có: $y' = \frac{3}{{{{\left( {x - 1} \right)}^2}}}$.

Nhận xét $y' > 0{\rm{ }}\forall x \in D$.

Ta có bảng biến thiên:

Vậy hàm số có giá trị lớn nhất bằng $\frac{1}{2}$ khi $x = 3$ và không có giá trị nhỏ nhất.

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 17 SGK Toán 12 Cánh diều

Cho hàm số $y = f\left( x \right) = 2{x^3} - 6x,x \in \left[ { - 2;2} \right]$ có đồ thị là đường cong ở Hình 9.

a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị $M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)$ bằng bao nhiêu.

b) Giải phương trình $f'\left( x \right) = 0$ với $x \in \left( { - 2;2} \right)$

c) Tính các giá trị của hàm số $f\left( x \right)$ tại hai đầu mút $- 2;2$ và tại các điểm $x \in \left( { - 2;2} \right)$ mà ở đó $f'\left( x \right) = 0$

d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c

Lời giải chi tiết:

a) Ta có: $\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 4\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 4\end{array} \right.$.

b) Ta có: $f'\left( x \right) = 6{x^2} - 6$.

Xét $f'\left( x \right) = 0 \Leftrightarrow x = \pm 1$.

c) Ta có:$\left\{ \begin{array}{l}f\left( 2 \right) = f\left( { - 1} \right) = 4\\f\left( { - 2} \right) = f\left( 1 \right) = - 4\end{array} \right.$.

d) Nhận xét: $\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( 2 \right) = f\left( { - 1} \right)\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( { - 2} \right) = f\left( 1 \right)\end{array} \right.$.

LT3

Trả lời câu hỏi Luyện tập 3 trang 18 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right) = \sin 2x - 2x$ trên đoạn $\left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right]$.

Phương pháp giải:

B1: Tìm các điểm ${x_1},{x_2},...,{x_n}$ thuộc khoảng $\left( {a;b} \right)$ mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.

B2: Tính $f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( a \right),f\left( b \right)$

B3: So sánh các giá trị tìm được ở bước 2 và kết luận

Lời giải chi tiết:

Ta có: $f'\left( x \right) = 2\cos 2x - 2$.

Xét $f'\left( x \right) = 0 \Leftrightarrow x = \pi$.

Ta có $f\left( {\frac{\pi }{2}} \right) = - \pi ,f\left( \pi \right) = - 2\pi ,f\left( {\frac{{3\pi }}{2}} \right) = - 3\pi$

Vậy hàm số $f\left( x \right) = \sin 2x - 2x$ có giá trị nhỏ nhất bằng $- 3\pi$ khi $x = \frac{{3\pi }}{2}$ và có giá trị lớn nhất bằng $- \pi$ khi $x = \frac{\pi }{2}$ .