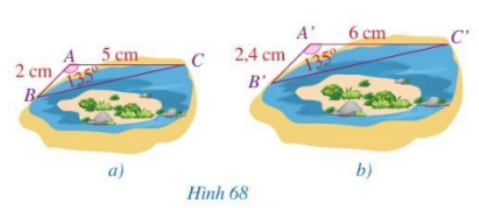
Giải mục 1 trang 79, 80 SGK Toán 8 – Cánh diềuQuan sát hình 68 và so sánh: Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên Lựa chọn câu để xem lời giải nhanh hơn HĐ1 Quan sát hình 68 và so sánh: a) Các tỉ số \(\frac{{A'B'}}{{AB}}\) và \(\frac{{A'C'}}{{AC}}\) b) Các góc \(\widehat A\) và \(\widehat {A'}\)
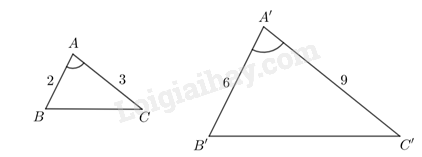
Phương pháp giải: Quan sát hình và so sánh các góc và tỉ số các cạnh. Lời giải chi tiết: a) Ta có: \(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2,4}{{2}} = \frac{6}{5}\\\frac{{A'C'}}{{AC}} = \frac{6}{5}\end{array}\) Vậy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) b) Ta có: \(\widehat A = \widehat {A'} = 135^\circ \) LT1 Cho hai tam giác ABC và A’B’C’ thỏa mãn \(AB = 2,AC = 3,A'B' = 6,A'C' = 9\) và \(\widehat A = \widehat {A'}\). Chứng minh \(\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}\). Phương pháp giải: Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ hai rồi suy ra các góc bằng nhau theo định nghĩa tam giác đồng dạng. Lời giải chi tiết:
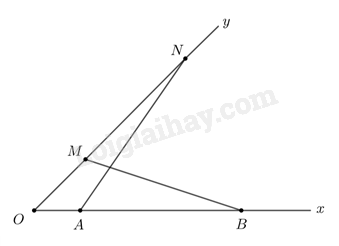
Ta thấy \(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{2}{6} = \frac{1}{3}\\\frac{{AC}}{{A'C'}} = \frac{3}{9} = \frac{1}{3}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\end{array}\) Xét tam giác ABC và tam giác A’B’C’ có: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) và \(\widehat A = \widehat {A'}\) \( \Rightarrow \Delta ABC \backsim \Delta A'B'C'\) (c-g-c) \( \Rightarrow \)\(\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}\) LT2 Cho góc \(xOy\). Trên tia Ox lấy các điểm A, B sao cho \(OA = 2cm,\,\,OB = 9cm\). Trên tia Oy lấy các điểm M, N sao cho \(OM = 3cm,\,\,ON = 6cm\). ChỨNG minh \(\widehat {OBM} = \widehat {ONA}\). Phương pháp giải: Chứng minh hai tam giác OAN và OMB đồng dạng theo trường hợp đồng dạng thứ hai rồi suy ra các góc bằng nhau theo định nghía tam giác đồng dạng. Lời giải chi tiết:
Ta thấy \(\begin{array}{l}\frac{{OA}}{{OM}} = \frac{2}{3};\,\,\frac{{ON}}{{OB}} = \frac{6}{9} = \frac{2}{3}\\ \Rightarrow \frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\end{array}\) Xét tam giác OAN và tam giác OMB có: \(\frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\) và \(\widehat O\) chung \( \Rightarrow \Delta OAN \backsim \Delta OMB\) (c-g-c) \( \Rightarrow \widehat {OBM} = \widehat {ONA}\)
|