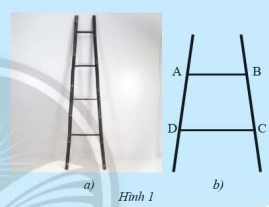
Giải mục 1 trang 68, 69 SGK Toán 8 – Chân trời sáng tạo

HĐ 1

Tứ giác \(ABCD\) (Hình 1b) là hình vẽ minh họa một phần của chiếc thang ở Hình 1a. Nêu nhận xét của em về hai cạnh \(AB\) và \(CD\) của tứ giác này.

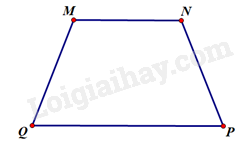
Phương pháp giải:

Quan sát, sử dụng kiến thức về hai đường thẳng song song

Lời giải chi tiết:

Hai cạnh \(AB\) và \(CD\) song song với nhau

TH 1

Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.

a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)

b) \(\widehat P = \widehat Q = 110^\circ \)

Phương pháp giải:

Sử dụng kiến thức về hình thang, hình thang cân, hình thang vuông

Lời giải chi tiết:

a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)

Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)

b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.

Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)

VD 1

Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo \(\widehat A\) và \(\widehat B\).

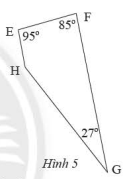
Phương pháp giải:

Sử dụng định nghĩa hình thang cân.

Lời giải chi tiết:

Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)

Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)

\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)

Mà \(\widehat A = \widehat B\) (cmt)

Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)

VD 2

Tứ giác \(EFGH\) có các góc cho như trong Hình 5.

a) Chứng minh rằng \(EFGH\) là hình thang

b) Tìm góc chưa biết của tứ giác

Phương pháp giải:

a) Chứng minh \(EH\) // \(FG\)

b) Sử dụng định lý tổng bốn góc của tứ giác bằng \(360^0\)

Lời giải chi tiết:

a) Ta có:

\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ + 85^\circ = 180^\circ \)

Mà hai góc ở vị trí Trong cùng phía

Suy ra \(EH\;{\rm{//}}\;FG\)

Suy ra: \(EFGH\) là hình thang

b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)

\(\begin{array}{l}95^\circ + 85^\circ + 27^\circ + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)