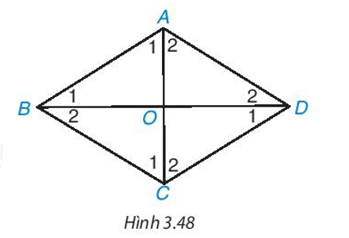
Giải mục 1 trang 67, 68 SGK Toán 8 tập 1 - Kết nối tri thứcHình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi. Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Lựa chọn câu để xem lời giải nhanh hơn Câu hỏi Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi. Phương pháp giải: Dựa vào định nghĩa hình thoi Lời giải chi tiết: Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau. Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau: - Hình thoi có hai góc đối bằng nhau. - Hình thoi có các cặp cạnh đối song song. - Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường. HĐ1 Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48).
a) ∆ABD có cân tại A không? b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao? Phương pháp giải: Dựa vào định nghĩa hình thoi. Lời giải chi tiết: a) Vì tứ giác ABCD là hình thoi nên AB = AD. Suy ra ∆ABD có cân tại A. b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA. Xét ∆ABC và ∆ADC có: AB = AD (chứng minh trên); BC = CD (chứng minh trên); Cạnh AC chung. Do đó ∆ABC = ∆ADC (c.c.c) Suy ra \(\)\(\widehat {{A_1}} = \widehat {{A_2}}\)(hai góc tương ứng) Hay AC là đường phân giác của góc A. Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao. Khi đó AO ⊥ BD hay AC ⊥ BD. Vậy AC vuông góc với BD và AC là đường phân giác của góc A. Câu hỏi 2 Hãy viết giả thiết, kết luận của câu c trong Định lí 2. Phương pháp giải: Vẽ hình và viết giả thiết kết luận Lời giải chi tiết:
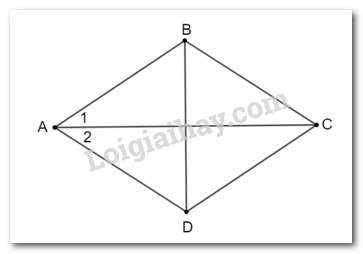
Giả thiết, kết luận của Định lí 2. a)
Ta có thể viết giả thiết đối với các cặp cạnh kề khác, chẳng hạn như: Hình bình hành ABCD có BC = CD hoặc CD = DA hoặc DA = AB. b)
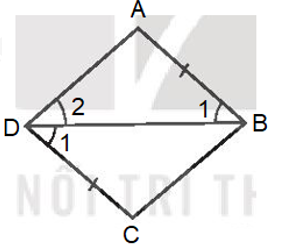
c)
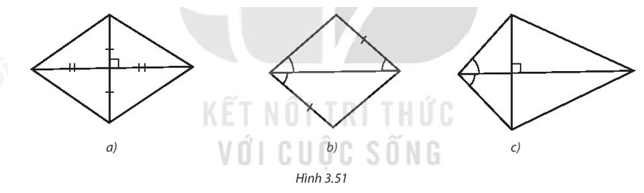
Ta có thể viết giả thiết tương tự đối với tia phân giác góc B hoặc góc C hoặc góc D. Luyện tập 1 Trong Hình 3.51, hình nào là hình thoi? Vì sao? Phương pháp giải: Quan sát hình 3.51 và dựa vào các dấu hiệu nhận biết hình thoi Lời giải chi tiết: • Hình 3.51a)
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi. • Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD. Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên AB // CD. Mà AB = CD nên tứ giác ABCD là hình bình hành. Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay DB là tia phân giác của \(\widehat {A{\rm{D}}C}\) Khi đó, hình bình hành ABCD có DB là tia phân giác của \(\widehat {A{\rm{D}}C}\). Do đó tứ giác ABCD là hình thoi. • Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác. Từ đó ta suy ra tứ giác đã cho không phải là hình thoi. Vậy Hình 3.51a và Hình 3.51b là hình thoi.
|