Giải đề thi học kì 2 toán lớp 11 năm 2019 - 2020 trường THPT Phú Lương - Thái NguyênGiải chi tiết đề thi học kì 2 môn toán lớp 11 năm 2019 - 2020 trường THPT Phú Lương - Thái Nguyên với cách giải nhanh và chú ý quan trọng Câu 1. Giới hạn \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} - 1}}{x}\) bằng A. 2. B. 3. C. \(\frac{1}{2}\). D. -2. Câu 2. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\). Biết \(SA = SC,\,SB = SD\). Tìm khẳng định sai ? A. \(BD \bot (SAC).\) B. \(CD \bot AC.\) C. \(SO \bot (ABCD).\) D. \(AC \bot (SBD).\) Câu 3. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 2}}\,\,\,\,khi\,\,\,x \ne 2\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,x = 2\end{array} \right..\) Tìm tất cả các giá trị của tham số \(m\) để hàm số đã cho liên tục tại \({x_0} = 2.\) A. \(m = - 2.\) B. \(m = 1.\) C. \(m = \pm \sqrt 2 .\) D. \(m = 2.\) Câu 4. Tiếp tuyến của đồ thị hàm số \(y = \frac{{{x^3}}}{3} - {x^2} - 2x\) có hệ số góc \(k = - 3\) có phương trình là A. \(y = - 3x + \frac{1}{3}.\) B. \(y = - 3x - \frac{1}{3}.\) C. \(y = - 9x + 43.\) D. \(y = - 3x - 11.\) Câu 5. Cho hàm số \(f(x) = \frac{1}{3}{x^3} + \frac{1}{2}{x^2} - 12x - 1\). Giải phương trình \(f'(x) = 0\). A. \(\left\{ { - 4;3} \right\}\) B. \(\left[ { - 3;4} \right]\). C. \(\left[ { - 4;3} \right]\). D. \(\left( { - \infty ; - 3} \right] \cup \left[ {4; + \infty } \right)\). Câu 6. Cho các hàm số \(u = u(x),v = v(x)\). Trong các công thức sau, công thức nào sai? A. \(\left( {u.v} \right)' = u'.v - u.v'\) B. \(\left( {\frac{u}{v}} \right)' = \frac{{u'.v - u.v'}}{{{v^2}}},\)\(v = v(x) \ne 0\) C. \(\left( {u + v} \right)' = u' + v'\) D. \(\left( {u - v} \right)' = u' - v'\) Câu 7. Đạo hàm của hàm số \(y = {x^4} + 3{x^2} - x + 1\) là A. \(y' = 4{x^3} - 6{x^2} + x\). B. \(y' = 4{x^3} + 3{x^2} - x\). C. \(y' = 4{x^3} + 6x - 1\). D. \(y' = 4{x^3} - 6x + 1\). Câu 8. Giới hạn\(\mathop {\lim }\limits_{x \to {1^ - }} \frac{5}{{x - 1}}\) bằng A. 2. B. \( - 5\). C. \( - \infty \). D. \( + \infty \). Câu 9. Đạo hàm của hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) là A. \(y' = - \frac{3}{{{{\left( {x + 1} \right)}^2}}}\) B. \(y' = - \frac{3}{{{{\left( {x - 1} \right)}^2}}}\). C. \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}\). D. \(y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\). Câu 10. Cho hàm số \(f(x) = {\left( {{x^2} - 3x} \right)^2}\). Tính \(f'(1)\). A. \(4\). B. \( - 12\). C. \(1\). D. \( - 1\). Câu 11. Một chất điểm chuyển động có phương trình \(s = 2{t^3} + {t^2} + 1\) (t tính bằng giây, s tính bằng mét). Vận tốc của chất điểm tại thời điểm \({t_0} = 2\) (giây) bằng A. \({\rm{19 m/s}}{\rm{.}}\) B. \({\rm{29 m/s}}{\rm{.}}\) C. \({\rm{28 m/s}}{\rm{.}}\) D. \({\rm{21 m/s}}{\rm{.}}\) Câu 12. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(SA \bot \left( {ABC} \right)\), \(SA = a,\) \({\rm{ }}AC = 2a,\) \({\rm{ }}BC = a\sqrt 3 \). Góc giữa \(SC\) và \(\left( {ABC} \right)\) là A. \(\widehat {CSB}.\) B. \(\widehat {CSA}.\) C. \(\widehat {SCB}.\) D. \(\widehat {SCA}.\) Câu 13. Cho hình lập phương \(ABCD.EFGH\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và\(\overrightarrow {DH} \). A. \(60^\circ \). B. \(45^\circ \). C. \(90^\circ \). D. \(120^\circ \). Câu 14. Trong các mệnh đề sau, mệnh đề nào đúng? A. \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos (\overrightarrow u ,\overrightarrow v ).\) B. \(\overrightarrow u .\overrightarrow v = \overrightarrow u .\overrightarrow v .\sin (\overrightarrow u ,\overrightarrow v ).\) C. \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\) D. \(\overrightarrow u .\overrightarrow v = \overrightarrow u .\overrightarrow v .\cos (\overrightarrow u ,\overrightarrow v ).\) Câu 15. Giới hạn \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{x - 3}}\) bằng A. 5. B. 6. C. 8. D. 7. Câu 16. Trong các mệnh đề sau, mệnh đề nào sai ? A. \(\lim \frac{1}{{{n^k}}} = 0\)\(\left( {k \ge 1} \right)\). B. \(\lim {q^n} = + \infty \) nếu \(q > 1\) . C. \(\lim {q^n} = + \infty \) nếu \(\left| q \right| < 1\). D. \(\lim {n^k} = + \infty \) với \(k\) nguyên dương. Câu 17. Trong các hàm số sau, hàm số nào liên tục trên \(\mathbb{R}\)? A. \(y = {x^3} - 2x + 4.\) B. \(y = \sqrt {2x - 1} .\) C. \(y = \tan x.\) D. \(y = \frac{{x + 2}}{{x - 1}}.\) Câu 18. Cho hình chóp S.ABC, gọi G là trọng tâm tam giác ABC. Tìm mệnh đề đúng trong các mệnh đề sau: A. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 4\overrightarrow {SG} \) B. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SG} \) C. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 2\overrightarrow {SG} \) D. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \). Câu 19. Biết \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + m\;x + 2019} + x} \right) = - 3\). Giá trị của \(m\) bằng A. -6. B. 3. C. -3. D. 6. Câu 20. Đạo hàm của hàm số \(y = \sin ({x^2} + 1)\) bằng: A. \(y' = 2x\sin ({x^2} + 1)\). B. \(y' = 2x\cos ({x^2} + 1)\). C. \(y' = 2\cos ({x^2} + 1)\) . D. \(y' = ({x^2} + 1)\cos (2x)\). Câu 21. Dãy số \(({u_n})\) với \({u_n} = \frac{{{3^n} + {{2.5}^n}}}{{{4^n} + {5^n}}}\)có giới hạn bằng A. 4. B. 2. C. 3. D. 5. Câu 22. Trong các khẳng định sau, khẳng định nào sai? A. Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\). B. Một đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng còn lại. C. Trong không gian, hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau. D. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. Câu 23. Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } ( - {x^3} + 2{x^2} - x + 1)\) bằng A. 1. B. \( - \infty \). C. -1. D. \( + \infty \). Câu 24. Tính đạo hàm của hàm số \(y = \tan 3x\). A. \(y' = - \frac{3}{{{{\cos }^2}3x}}\) B. \(y' = - \frac{3}{{si{n^2}3x}}\). C. \(y' = \frac{{3x}}{{{{\cos }^2}3x}}\). D. \(y' = \frac{3}{{{{\cos }^2}3x}}\). II/ TỰ LUẬN (4 điểm): (Học sinh ghi mã đề vào bài thi) Câu 1 (1 điểm) a) Tính đạo hàm của hàm số sau: \(y = \left( {{x^2} - 5x} \right)\left( {x + 2} \right)\) b) Xét tính liên tục của hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2}\,\, + \,\,3x\,\, + 2}}{{x\,\,\, + 2}}\,\,\,khi\,\,\,x\, \ne \, - 2\\2\,\,\,\,\,\begin{array}{*{20}{c}}{}&{}\end{array}\begin{array}{*{20}{c}}{}&{khi}\end{array}\,\,x\, = \, - 2\end{array} \right.\) tạiđiểm\({x_0} = - 2\). Câu 2 (0,5 điểm) Cho hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} + 3x\). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ bằng \( - 1\). Câu 3( 1,5 điểm) Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy, \(SA = a\sqrt 6 \). a) Chứng minh rằng \(BD \bot (SAC)\). b) Tính góc giữa cạnh \(SC\) và \((ABCD).\) Câu 4(1 điểm) Cho hàm số \(y = - x - 1\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của \(\left( C \right)\), biết tiếp tuyến tạo với hai trục tọa độ một tam giác có diện tích bằng \({x_0}\). HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn xemloigiai.com PHẦN I: TRẮC NGHIỆM (6 điểm)
Câu 1 (TH): Phương pháp: Nhân cả tử và mẫu với biểu thức liên hợp. Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} - 1}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{{x\left( {\sqrt {x + 1} + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{x + 1 - 1}}{{x\left( {\sqrt {x + 1} + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{x}{{x\left( {\sqrt {x + 1} + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt {x + 1} + 1}}\\ = \frac{1}{{\sqrt {0 + 1} + 1}} = \frac{1}{2}\end{array}\) Chọn C Câu 2(TH): Phương pháp: Nhận xét tính đúng sai của từng đáp án, sử dụng lý thuyết: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó. Cách giải:
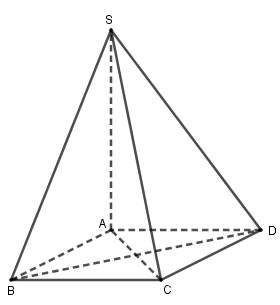
ABCD là hình thoi nên \(AC \bot BD\) tại trung điểm O của mỗi đường. SA=SC nên tam giác SAC cân tại S\( \Rightarrow SO \bot AC\) SB=SD nên tam giác SBD cân tại S\( \Rightarrow SO \bot BD\) Ta có: \(\left\{ \begin{array}{l}SO \bot AC\\SO \bot BD\end{array} \right.\) \( \Rightarrow SO \bot \left( {ABCD} \right)\) nên C đúng. Lại có: \(\left\{ \begin{array}{l}BD \bot SO\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\) nên A đúng. \(\left\{ \begin{array}{l}AC \bot SO\\AC \bot BD\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right)\) nên D đúng. Đáp án B sai vì CD không thể vuông góc với AC. Chọn B Câu 3 (TH): Phương pháp: Hàm số \(y = f\left( x \right)\) liên tục tại \({x_0}\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) Cách giải: Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x + 2}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {x - 1} \right) = 2 - 1 = 1\\f\left( 2 \right) = m\end{array}\) Hàm số liên tục tại \({x_0} = 2\) \(\begin{array}{l} \Leftrightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\\ \Leftrightarrow 1 = m\end{array}\) Chọn B Câu 4 (TH): Phương pháp: - Tính đạo hàm \(y'\). - Giải phương trình \(y'\left( {{x_0}} \right) = - 3\) tìm \({x_0}\). - Thay \({x_0}\) vào hàm số tìm \({y_0}\) và viết pttt: \(y = k\left( {x - {x_0}} \right) + {y_0}\). Cách giải: Ta có: \(y' = {x^2} - 2x - 2\). Gọi \(M\left( {{x_0};{y_0}} \right)\) là tiếp điểm. Hệ số góc \(k = - 3\) \( \Leftrightarrow y'\left( {{x_0}} \right) = - 3\) \(\begin{array}{l} \Leftrightarrow x_0^2 - 2{x_0} - 2 = - 3\\ \Leftrightarrow x_0^2 - 2{x_0} + 1 = 0\\ \Leftrightarrow {x_0} = 1\\ \Rightarrow {y_0} = \frac{1}{3} - 1 - 2 = - \frac{8}{3}\end{array}\) \( \Rightarrow M\left( {1; - \frac{8}{3}} \right)\) Tiếp tuyến tại M là: \(y = - 3\left( {x - 1} \right) - \frac{8}{3}\) hay \(y = - 3x + \frac{1}{3}\). Chọn A Câu 5 (TH): Phương pháp: Tính \(f'\left( x \right)\) và giải phương trình \(f'\left( x \right) = 0\). Cách giải: Ta có: \(f'\left( x \right) = {x^2} + x - 12\) \(\begin{array}{l}f'\left( x \right) = 0 \Leftrightarrow {x^2} + x - 12 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 4\end{array} \right.\end{array}\) Chọn A Câu 6 (TH): Phương pháp: Sử dụng công thức đạo hàm của tổng, hiệu, tích, thương các hàm số. Cách giải: Ta có: \(\left( {u.v} \right)' = u'.v + u.v'\) nên A sai. \(\left( {\frac{u}{v}} \right)' = \frac{{u'.v - u.v'}}{{{v^2}}}\) với \(v = v(x) \ne 0\) nên B đúng. \(\left( {u \pm v} \right)' = u' \pm v'\) nên C, D đúng. Chọn A Câu 7 (TH): Phương pháp: Đạo hàm hàm số cơ bản: \(\left( {{x^n}} \right)' = n{x^{n - 1}}\). Cách giải: \(\begin{array}{l}y = {x^4} + 3{x^2} - x + 1\\y' = \left( {{x^4}} \right)' + \left( {3{x^2}} \right)' - \left( x \right)' + \left( 1 \right)'\\ = 4{x^3} + 3.2x - 1 + 0\\ = 4{x^3} + 6x - 1\end{array}\) Chọn C Câu 8 (TH): Phương pháp: Sử dụng quy tắc tính giới hạn dạng \(\frac{L}{0}\) Cách giải: Ta có: \(5 > 0\) và \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left( {x - 1} \right) = 0\\x - 1 < 0,\forall x < 1\end{array} \right.\) nên \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{5}{{x - 1}} = - \infty \) Chọn C Câu 9 (TH): Phương pháp: Sử dụng công thức đạo hàm của một thương \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) Hoặc đạo hàm hàm số phân thức bậc nhất trên bậc nhất: \(\left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ac - bd}}{{{{\left( {cx + d} \right)}^2}}}\). Cách giải: Ta có: \(\begin{array}{l}y = \frac{{2x + 1}}{{x - 1}}\\y' = \frac{{\left( {2x + 1} \right)'\left( {x - 1} \right) - \left( {2x + 1} \right)\left( {x - 1} \right)'}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{2\left( {x - 1} \right) - \left( {2x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{2x - 2 - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}}\end{array}\) Chọn B Câu 10 (TH): Phương pháp: Tính \(f'\left( x \right)\) theo công thức hàm hợp \(\left[ {f\left( u \right)} \right]' = u'f'\left( u \right)\) Thay \(x = 1\) vào \(f'\left( x \right)\) tính \(f'\left( 1 \right)\). Cách giải: Ta có: \(\begin{array}{l}f'\left( x \right) = 2\left( {{x^2} - 3x} \right)\left( {{x^2} - 3x} \right)'\\ = 2\left( {{x^2} - 3x} \right)\left( {2x - 3} \right)\end{array}\) \( \Rightarrow f'\left( 1 \right) = 2\left( {{1^2} - 3.1} \right)\left( {2.1 - 3} \right)\) \( = 4\) Chọn A Câu 11 (TH): Phương pháp: Sử dụng công thức \(v = s'\left( t \right)\) rồi thay \(t = 2\) vào tính \(v\left( 2 \right)\). Cách giải: Ta có: \(\begin{array}{l}v\left( t \right) = s'\left( t \right) = 6{t^2} + 2t\\ \Rightarrow v\left( 2 \right) = {6.2^2} + 2.2 = 28\end{array}\) Chọn C Câu 12 (TH): Phương pháp: Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng. Cách giải:
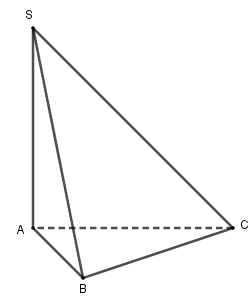
Ta có: \(SA \bot \left( {ABC} \right)\) \( \Rightarrow AC\) là hình chiếu của \(SC\) lên \(\left( {ABC} \right)\) \( \Rightarrow \) góc giữa SC và (ABC) bằng góc giữa SC và AC, chính là góc \(\widehat {SCA}\). Chọn D Câu 13 (TH): Phương pháp: Dựng hình và nhận xét. Cách giải:
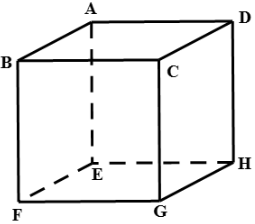
Ta có: \(\left\{ \begin{array}{l}DH \bot AD\\DH \bot DC\end{array} \right.\) \( \Rightarrow DH \bot \left( {ABCD} \right) \Rightarrow DH \bot AB\) Do đó góc giữa \(\overrightarrow {AB} \) và \(\overrightarrow {DH} \) bằng \({90^0}\). Chọn C Câu 14 (TH): Phương pháp: Sử dụng công thức tính tích vô hướng của hai véc tơ. Cách giải: Ta có: \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos (\overrightarrow u ,\overrightarrow v ).\) Chọn A Câu 15 (TH): Phương pháp: Khử dạng vô định bằng cách phân tích tử thức thành nhân tử. Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{x - 3}}\\ = \mathop {\lim }\limits_{x \to 3} \left( {x + 3} \right) = 3 + 3 = 6\end{array}\) Chọn B Câu 16 (TH): Phương pháp: Sử dụng giới hạn các dãy số thường gặp. Cách giải: \(\lim \frac{1}{{{n^k}}} = 0\) với \(k \ge 1\) nên A đúng. \(\lim {q^n} = + \infty \) nếu \(q > 1\) nên B đúng. \(\lim {q^n} = 0\) nếu \(\left| q \right| < 1\) nên C sai. \(\lim {n^k} = + \infty \) với \(k\) nguyên dương nên D đúng. Chọn C Câu 17 (TH): Phương pháp: Các hàm số đa thức, phân thức, lượng giác liên tục trên TXĐ. Cách giải: Hàm số \(y = {x^3} - 2x + 4\) là hàm đa thức có TXĐ \(D = \mathbb{R}\) nên liên tục trên \(\mathbb{R}\). Ngoài ra các hàm số còn lại đều có TXĐ không phải \(\mathbb{R}\) nên không liên tục trên \(\mathbb{R}\). Chọn A Câu 18 (TH): Phương pháp: Sử dụng tính chất trọng tâm: Điểm G là trọng tâm tam giác ABC nếu và chỉ nếu \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) Cách giải: G là trọng tâm tam giác ABC nên: \(\begin{array}{l}\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {SA} - \overrightarrow {SG} + \overrightarrow {SB} - \overrightarrow {SG} + \overrightarrow {SC} - \overrightarrow {SG} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} - 3\overrightarrow {SG} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \end{array}\) Chọn D Câu 19 (TH): Phương pháp: Tính giới hạn vế trái bằng cách nhân chia với biểu thức liên hợp. Cách giải: Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + m\;x + 2019} + x} \right)\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + m\;x + 2019 - {x^2}}}{{\sqrt {{x^2} + m\;x + 2019} - x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{m\;x + 2019}}{{\sqrt {{x^2} + m\;x + 2019} - x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{m\;x + 2019}}{{\left| x \right|\sqrt {1 + \frac{m}{x} + \frac{{2019}}{{{x^2}}}} - x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {m\; + \frac{{2019}}{x}} \right)}}{{ - x\sqrt {1 + \frac{m}{x} + \frac{{2019}}{{{x^2}}}} - x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{m\; + \frac{{2019}}{x}}}{{ - \sqrt {1 + \frac{m}{x} + \frac{{2019}}{{{x^2}}}} - 1}}\\ = \frac{m}{{ - 1 - 1}} = - \frac{m}{2}\end{array}\) Mà \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + m\;x + 2019} + x} \right) = - 3\) \( \Rightarrow - \frac{m}{2} = - 3 \Leftrightarrow m = 6\) Chọn D Câu 20 (TH): Phương pháp: Sử dụng công thức \(\left( {\sin u} \right)' = u'\cos u\) Cách giải: \(\begin{array}{l}\left[ {\sin \left( {{x^2} + 1} \right)} \right]'\\ = \left( {{x^2} + 1} \right)'\cos \left( {{x^2} + 1} \right)\\ = 2x\cos \left( {{x^2} + 1} \right)\end{array}\) Chọn B Câu 21 (TH): Phương pháp: Chia cả tử và mẫu cho \({5^n}\) và sử dụng giới hạn \(\lim {q^n} = 0\) với \(\left| q \right| < 1\). Cách giải: \(\begin{array}{l}\lim {u_n} = \lim \frac{{{3^n} + {{2.5}^n}}}{{{4^n} + {5^n}}}\\ = \lim \frac{{{{\left( {\frac{3}{5}} \right)}^n} + 2}}{{{{\left( {\frac{4}{5}} \right)}^n} + 1}} = \frac{{0 + 2}}{{0 + 1}} = 2\end{array}\) Chọn B Câu 22 (TH): Phương pháp: Sử dụng lý thuyết hai đường thẳng vuông góc. Cách giải: Đáp án A: đúng. Đáp án B: đúng. Đáp án C: đúng. Đáp án D: sai trong trường hợp hai đường thẳng này cắt nhau, cùng nằm trong mặt phẳng vuông góc với đường thẳng kia. Chọn Câu 23 (TH): Phương pháp: Đặt \({x^3}\) ra làm nhân tử chung. Cách giải: Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 2{x^2} - x + 1} \right)\\ = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( { - 1 + \frac{2}{x} - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right]\end{array}\) Vì \(\mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \) và \(\mathop {\lim }\limits_{x \to - \infty } \left( { - 1 + \frac{2}{x} - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)\) \( = - 1 < 0\) nên \(\mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 2{x^2} - x + 1} \right)\) \( = + \infty \) Chọn D Câu 24 (TH): Phương pháp: Sử dụng công thức \(\left( {\tan u} \right)' = \frac{{u'}}{{{{\cos }^2}u}}\) Cách giải: \(\begin{array}{l}y = \tan 3x\\y' = \frac{{\left( {3x} \right)'}}{{{{\cos }^2}3x}} = \frac{3}{{{{\cos }^2}3x}}\end{array}\) Chọn D PHẦN II: TỰ LUẬN (4 điểm) Câu 1 (VD): Phương pháp: a) Sử dụng công thức đạo hàm của một tích: \(\left( {uv} \right)' = u'v + uv'\) b) Hàm số \(y = f\left( x \right)\) liên tục tại \({x_0}\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) Cách giải: a) Tính đạo hàm của hàm số sau:\(y = \left( {{x^2} - 5x} \right)\left( {x + 2} \right)\) Ta có: \(\begin{array}{l}y = \left( {{x^2} - 5x} \right)\left( {x + 2} \right)\\ = {x^3} - 5{x^2} + 2{x^2} - 10x\\ = {x^3} - 3{x^2} - 10x\\y' = \left( {{x^3} - 3{x^2} - 10x} \right)'\\ = \left( {{x^3}} \right)' - \left( {3{x^2}} \right)' - \left( {10x} \right)'\\ = 3{x^2} - 3.2x - 10\\ = 3{x^2} - 6x - 10\end{array}\) Cách khác: \(\begin{array}{l}y = \left( {{x^2} - 5x} \right)\left( {x + 2} \right)\\y'\\ = \left( {{x^2} - 5x} \right)'\left( {x + 2} \right) + \left( {{x^2} - 5x} \right)\left( {x + 2} \right)'\\ = \left( {2x - 5} \right)\left( {x + 2} \right) + \left( {{x^2} - 5x} \right).1\\ = 2{x^2} - 5x + 4x - 10 + {x^2} - 5x\\ = 3{x^2} - 6x - 10\end{array}\) b) Xét tính liên tục của hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2}\,\, + \,\,3x\,\, + 2}}{{x\,\,\, + 2}}\,\,\,khi\,\,\,x\, \ne \, - 2\\2\,\,\,\,\,\begin{array}{*{20}{c}}{}&{}\end{array}\begin{array}{*{20}{c}}{}&{khi}\end{array}\,\,x\, = \, - 2\end{array} \right.\)tạiđiểm\({x_0} = - 2\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 3x + 2}}{{x + 2}}\\ = \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{x + 2}}\\ = \mathop {\lim }\limits_{x \to - 2} \left( {x + 1} \right) = - 2 + 1 = - 1\\f\left( { - 2} \right) = 2\end{array}\) Dễ thấy \( - 1 \ne 2\) \( \Rightarrow \mathop {\lim }\limits_{x \to - 2} f\left( x \right) \ne f\left( { - 2} \right)\) Vậy hàm số không liên tục tại \(x = - 2\). Câu 2 (VD): Phương pháp: - Thay \({x_0} = - 1\) tìm \({y_0}\). - Tính \(f'\left( x \right)\) và \(f'\left( { - 1} \right)\). - Thay vào công thức phương trình tiếp tuyến \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\). Cách giải: Cho hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} + 3x\). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ bằng \( - 1\). Ta có: \(f'\left( x \right) = 3{x^2} - 4x + 3\) Với \({x_0} = - 1\) thì \({y_0} = {\left( { - 1} \right)^3} - 2{\left( { - 1} \right)^2} + 3.\left( { - 1} \right)\) \( = - 6\) ta được điểm \(\left( { - 1; - 6} \right)\). \(f'\left( { - 1} \right) = 3.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 3\) \( = 10\) Tiếp tuyến tại điểm \(\left( { - 1; - 6} \right)\) là: \(y = 10\left( {x + 1} \right) - 6\) hay \(y = 10x + 4\). Vậy tiếp tuyến cần tìm là \(y = 10x + 4\). Câu 3 (VD): Phương pháp: a) Chứng minh \(BD \bot AC\) và \(BD \bot SA\). Từ đó suy ra \(BD \bot \left( {SAC} \right)\) Sử dụng lí thuyết: Một đường thẳng vuông góc với hai đường thẳng cắt nhau thì vuông góc với mặt phẳng chứa hai đường thẳng đó. b) Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng. Cách giải:
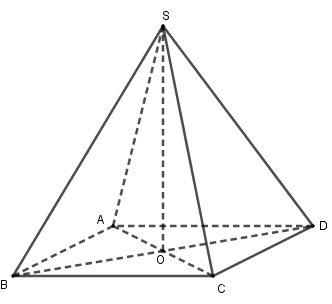
a) Chứng minh rằng \(BD \bot (SAC)\). ABCD là hình vuông nên \(BD \bot AC\) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\) Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\) (đpcm) b) Tính góc giữa cạnh \(SC\) và \((ABCD).\) Ta có: \(SA \bot \left( {ABCD} \right)\) nên AC là hình chiếu của SC lên mặt phẳng (ABCD) \( \Rightarrow \) góc giữa SC và (ABCD) bằng góc giữa SC và AC hay \(\widehat {SCA}\). ABCD là hình vuông nên \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) Tam giác SAC vuông tại A nên \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 6 }}{{a\sqrt 2 }} = \sqrt 3 \) \( \Rightarrow \widehat {SCA} = {60^0}\) Vậy góc giữa SC và (ABCD) bằng \({60^0}\). Câu 4 (VDC): Phương pháp: - Tính \(y'\) và viết phương trình tiếp tuyến \(\Delta \) của \(\left( C \right)\) tại một điểm \(M\left( {{x_0};{y_0}} \right)\) bất kì. - Cho \(x = 0\) tìm giao điểm A của \(\Delta \) với Oy. - Cho \(y = 0\) tìm giao điểm B của \(\Delta \) với Ox. - Sử dụng công thức tính diện tích tam giác OAB suy ra \({x_0}\). Từ đó suy ra phương trình tiếp tuyến cần tìm. Cách giải: Cho hàm số \(y = - x - 1\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của \(\left( C \right)\), biết tiếp tuyến tạo với hai trục tọa độ một tam giác có diện tích bằng \({x_0}\). Gọi \(M\left( {{x_0};{y_0}} \right)\) là tiếp điểm với \({y_0} = \frac{{2{x_0}}}{{{x_0} + 2}}\). \(\begin{array}{l}y' = \frac{{\left( {2x} \right)'\left( {x + 2} \right) - 2x\left( {x + 2} \right)'}}{{{{\left( {x + 2} \right)}^2}}}\\ = \frac{{2\left( {x + 2} \right) - 2x.1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{2x + 4 - 2x}}{{{{\left( {x + 2} \right)}^2}}}\\ = \frac{4}{{{{\left( {x + 2} \right)}^2}}}\end{array}\) Phương trình tiếp tuyến \(\Delta \) của \(\left( C \right)\) tại \(M\) là: \(\begin{array}{l}y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\\ = \frac{4}{{{{\left( {{x_0} + 2} \right)}^2}}}\left( {x - {x_0}} \right) + \frac{{2{x_0}}}{{{x_0} + 2}}\end{array}\) Cho \(x = 0\) thì \(\begin{array}{l}y = \frac{4}{{{{\left( {{x_0} + 2} \right)}^2}}}\left( {0 - {x_0}} \right) + \frac{{2{x_0}}}{{{x_0} + 2}}\\ = \frac{{ - 4{x_0}}}{{{{\left( {{x_0} + 2} \right)}^2}}} + \frac{{2{x_0}}}{{{x_0} + 2}}\\ = \frac{{ - 4{x_0} + 2x_0^2 + 4{x_0}}}{{{{\left( {{x_0} + 2} \right)}^2}}} = \frac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}}\end{array}\) Ta được điểm \(A\left( {0;\frac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}}} \right)\) là giao điểm của \(\Delta \) với \(Oy\). Cho \(y = 0\) thì \(\begin{array}{l}0 = \frac{4}{{{{\left( {{x_0} + 2} \right)}^2}}}\left( {x - {x_0}} \right) + \frac{{2{x_0}}}{{{x_0} + 2}}\\ \Rightarrow \frac{4}{{{{\left( {{x_0} + 2} \right)}^2}}}\left( {x - {x_0}} \right) = - \frac{{2{x_0}}}{{{x_0} + 2}}\\ \Rightarrow x - {x_0} = - \frac{{2{x_0}}}{{{x_0} + 2}}:\frac{4}{{{{\left( {{x_0} + 2} \right)}^2}}}\\ \Rightarrow x - {x_0} = \frac{{ - {x_0}\left( {{x_0} + 2} \right)}}{2}\\ \Rightarrow x = \frac{{ - {x_0}\left( {{x_0} + 2} \right)}}{2} + {x_0}\\ = \frac{{ - x_0^2 - 2{x_0} + 2{x_0}}}{2} = \frac{{ - x_0^2}}{2}\end{array}\) Ta được điểm \(B\left( { - \frac{{x_0^2}}{2};0} \right)\) là giao điểm của \(\Delta \) với \(Ox\). Vì \(A,B \ne O\) nên \({x_0} \ne 0\). Diện tích tam giác OAB là: \(\begin{array}{l}{S_{OAB}} = \frac{1}{2}OA.OB\\ = \frac{1}{2}\left| {\frac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}}} \right|.\left| { - \frac{{x_0^2}}{2}} \right| = \frac{1}{2}.\frac{{x_0^4}}{{{{\left( {{x_0} + 2} \right)}^2}}}\end{array}\) Do \({S_{OAB}} = \frac{1}{{18}}\) nên \(\begin{array}{l}\frac{1}{2}.\frac{{x_0^4}}{{{{\left( {{x_0} + 2} \right)}^2}}} = \frac{1}{{18}}\\ \Leftrightarrow 18x_0^4 = 2{\left( {{x_0} + 2} \right)^2}\\ \Leftrightarrow 9x_0^4 = {\left( {{x_0} + 2} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}3x_0^2 = {x_0} + 2\\3x_0^2 = - {x_0} - 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}3x_0^2 - {x_0} - 2 = 0\\3x_0^2 + {x_0} + 2 = 0\,\,\left( {VN} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} = - \frac{2}{3}\end{array} \right.\,\,\,\,\,\left( {TM} \right)\end{array}\) +) Với \({x_0} = 1\) thì \({y_0} = \frac{{2.1}}{{1 + 2}} = \frac{2}{3}\) và \(y'\left( 1 \right) = \frac{4}{{{{\left( {1 + 2} \right)}^2}}} = \frac{4}{9}\) ta có tiếp tuyến: \(y = \frac{4}{9}\left( {x - 1} \right) + \frac{2}{3}\) hay \(y = \frac{4}{9}x + \frac{2}{9}\) +) Với \({x_0} = - \frac{2}{3}\) thì \({y_0} = \frac{{2.\left( { - \frac{2}{3}} \right)}}{{ - \frac{2}{3} + 2}} = - 1\) và \(y'\left( { - \frac{2}{3}} \right) = \frac{4}{{{{\left( { - \frac{2}{3} + 2} \right)}^2}}} = \frac{9}{4}\) ta có tiếp tuyến: \(y = \frac{9}{4}\left( {x + \frac{2}{3}} \right) - 1\) hay \(y = \frac{9}{4}x + \frac{1}{2}\). Vậy có hai tiếp tuyến cần tìm là: \(\begin{array}{l}{\Delta _1}:y = \frac{4}{9}x + \frac{2}{9}\\{\Delta _2}:y = \frac{9}{4}x + \frac{1}{2}\end{array}\) xemloigiai.com
|