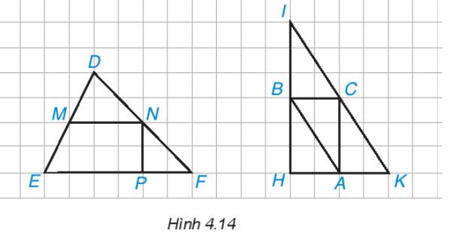
Giải câu hỏi trang 81, 82 SGK Toán 8 tập 1 - Kết nối tri thức

Câu hỏi

Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.

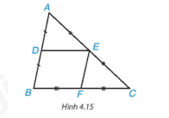
Phương pháp giải:

Quan sát hình 4.14

Lời giải chi tiết:

Quan sát Hình 4.14, ta thấy:

* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.

* Xét ∆IHK có:

• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.

• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.

• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.

Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.

HĐ1

Cho DE là đường trung bình của tam giác ABC (H.4.15)

Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.

Phương pháp giải:

Áp dụngđịnh lí Thalès đảo

Lời giải chi tiết:

Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;

AE = EC và E ∈ AC nên E là trung điểm của AC.

Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

HĐ2

Cho DE là đường trung bình của tam giác ABC (H.4.15)

Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE = \(\frac{1}{2}\)BC

Phương pháp giải:

Sử dụng dấu hiệu nhận biết hình bình hành.

Sử dụng tính chất của hình bình hành.

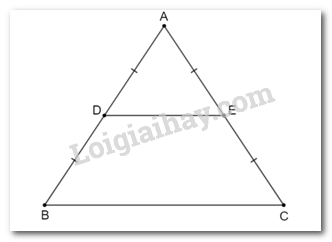
Lời giải chi tiết:

Chứng minh tương tự HĐ1, ta có EF // AB.

Xét tam giác DEFB có DE // BF, EF // BD

=> DEFB là hình bình hành.

=> DE = BF (hai cạnh tương ứng)

Mà F là trung điểm của BC => BF = \(\frac{1}{2}\)BC

=> DE = \(\frac{1}{2}\)BC

Luyện tập

Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?

Phương pháp giải:

Sử dụng tính chất đường trung bình để chứng minh:Tứ giác DECB có DE // BC suy ra tứ giác DECB là hình thang có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.

Lời giải chi tiết:

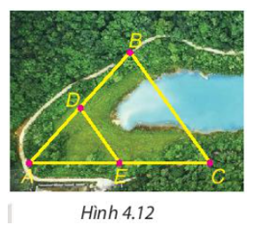
Tam giác ABC cân tại A nên \(\widehat B = \widehat C\)

Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.

Suy ra DE // BC nên tứ giác DECB là hình thang.

Hình thang DECB có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.

Vận dụng

Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?

Phương pháp giải:

Vận dụng tính chất đường trung bình trong tam giác

Lời giải chi tiết:

Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.

Suy ra DE là đường trung bình của tam giác ABC.

Do đó \(DE = \frac{1}{2}BC\) suy ra BC = 2DE = 2 . 500 = 1 000 (m)

Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.