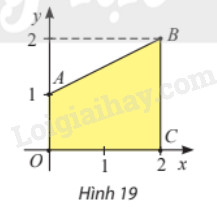
Giải bài tập 7 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo

Đề bài

Trong mặt phẳng toạ độ $Oxy$, cho hình thang $OABC$ có $A\left( {0;1} \right)$, $B\left( {2;2} \right)$ và $C\left( {2;0} \right)$ (hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang $OABC$ quanh trục $Ox$.

Lời giải chi tiết

Hình thang $OABC$ được giới hạn bởi các đường thẳng $AB$, $OC$ (trục hoành), $OA$ (trục tung, $x = 0$) và $BC$ $\left( {x = 2} \right)$.

Phương trình đường thẳng $AB$ là $y = f\left( x \right) = ax + b$. Do $A\left( {0;1} \right)$, $B\left( {2;2} \right)$ nên ta có hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{a.0 + b = 1}\\{a.2 + b = 2}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = 1\end{array} \right.$

Vậy phương trình đường thẳng $AB$ là $y = \frac{1}{2}x + 1$.

Thể tích khối tròn xoay khi quay hình thang $OABC$ quanh trục $Ox$ là:

$V = \pi \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} = \pi \int\limits_0^2 {\left( {\frac{1}{4}{x^2} + x + 1} \right)dx} = \pi \left. {\left( {\frac{{{x^3}}}{{12}} + \frac{{{x^2}}}{2} + x} \right)} \right|_0^2 = \frac{{14}\pi}{3}$.