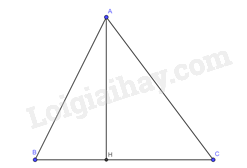
Giải bài tập 2 trang 86 SGK Toán 9 tập 1 - Cánh diềuCho tam giác (ABC) có đường cao (AH = 6cm,widehat B = 40^circ ,widehat C = 35^circ ). Tính độ dài các đoạn thẳng (AB,BH,AC,BC) (làm tròn kết quả đến hàng phần mười của centimét). Tổng hợp đề thi giữa kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN Đề bài Cho tam giác \(ABC\) có đường cao \(AH = 6cm,\widehat B = 40^\circ ,\widehat C = 35^\circ \). Tính độ dài các đoạn thẳng \(AB,BH,AC,BC\) (làm tròn kết quả đến hàng phần mười của centimét). Phương pháp giải - Xem chi tiết Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Lời giải chi tiết
Xét tam giác \(ABH\) vuông tại \(H\), ta có: +) \(AB = \frac{{AH}}{{\sin 40^\circ }} = \frac{6}{{\sin 40^\circ }} \approx 9,3\left( {cm} \right)\). +) \(BH = \frac{{AH}}{{\tan 40^\circ }} = \frac{6}{{\tan 40^\circ }} \approx 7,2\left( {cm} \right)\). Xét tam giác \(AHC\) vuông tại \(H\), ta có: +) \(AC = \frac{{AH}}{{\sin 35^\circ }} = \frac{6}{{\sin 35^\circ }} \approx 10,5\left( {cm} \right)\). +) \(CH = \frac{{AH}}{{\tan 35^\circ }} = \frac{6}{{\tan 35^\circ }} \approx 8,6\left( {cm} \right)\). Ta có: \(BC = BH + HC \approx 7,2 + 8,6 \approx 15,8\left( {cm} \right)\).
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
