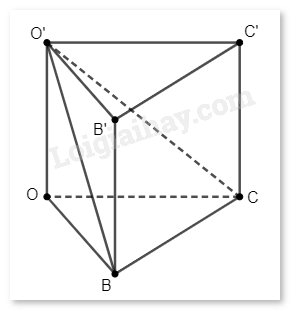
Giải bài tập 12 trang 60 SGK Toán 12 tập 2 - Chân trời sáng tạoTrong không gian (Oxyz), cho hình lăng trụ đứng (OBC.O'B'C') có đáy là tam giác (OBC) vuông tại (O). Cho biết (Bleft( {3;0;0} right)), (Cleft( {0;1;0} right)), (O'left( {0;0;2} right)). Tính góc giữa: a) hai đường thẳng (BO') và (B'C). b) hai mặt phẳng (left( {O'BC} right)) và (left( {OBC} right)). c) đường thẳng (B'C) và mặt phẳng (left( {O'BC} right)). Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O. Cho biết B(3;0;0), C(0;1;0), O'(0;0;2). Tính góc giữa: a) Hai đường thẳng BO' và B'C. b) Hai mặt phẳng (O'BC) và (OBC). c) Đường thẳng B'C và mặt phẳng (O'BC). Phương pháp giải - Xem chi tiết a) Chỉ ra \(\overrightarrow {BO'} \) và \(\overrightarrow {B'C} \) lần lượt là các vectơ chỉ phương của các đường thẳng \(BO'\) và \(B'C\), sau đó sử dụng công thức \(\cos \left( {BO',B'C} \right) = \left| {\cos \left( {\overrightarrow {BO} ',\overrightarrow {B'C} } \right)} \right|\). b) Với mặt phẳng \(\left( {O'BC} \right)\), ta cần chỉ ra một cặp vectơ chỉ phương, rồi tính tích có hướng để lần lượt tìm ra vectơ pháp tuyến \(\vec n\). Với mặt phẳng \(\left( {OBC} \right)\), chỉ ra rằng \(\overrightarrow {OO'} \) là một vectơ pháp tuyến của mặt phẳng đó. Từ đó suy ra \(\cos \left( {\left( {O'BC} \right),\left( {OBC} \right)} \right) = \left| {\cos \left( {\overrightarrow {OO'} ,\vec n} \right)} \right|\). c) Từ câu a và b, ta có \(\overrightarrow {B'C} \) là một vectơ chỉ phương của \(B'C\), \(\vec n\) là một vectơ pháp tuyến của mặt phẳng \(\left( {O'BC} \right)\). Suy ra \(\sin \left( {B'C,\left( {O'BC} \right)} \right) = \left| {\cos \left( {\overrightarrow {B'C} ,\vec n} \right)} \right|\). Lời giải chi tiết
a) Ta có toạ độ các điểm \(O\left( {0;0;0} \right)\), \(B\left( {3;0;0} \right)\), \(C\left( {0;1;0} \right)\), \(O'\left( {0;0;2} \right)\). Suy ra \(B'\left( {3;0;2} \right)\). Ta có \(\overrightarrow {BO'} = \left( { - 3;0;2} \right)\) là một vectơ chỉ phương của đường thẳng \(BO'\) và \(\overrightarrow {B'C} = \left( { - 3;1; - 2} \right)\) là một vectơ chỉ phương của đường thẳng \(B'C\). Suy ra: \(\cos \left( {BO',B'C} \right) = \left| {\cos \left( {\overrightarrow {BO} ',\overrightarrow {B'C} } \right)} \right| = \frac{{\left| {\left( { - 3} \right).\left( { - 3} \right) + 0.1 + 2.\left( { - 2} \right)} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {0^2} + {2^2}} .\sqrt {{{\left( { - 3} \right)}^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = \frac{5}{{\sqrt {182} }}\) Từ đó \(\left( {BO',B'C} \right) \approx {68^o}15'\). b) Mặt phẳng \(\left( {O'BC} \right)\) có cặp vectơ chỉ phương là \(\overrightarrow {BC} = \left( { - 3;1;0} \right)\) và \(\overrightarrow {BO'} = \left( { - 3;0;2} \right)\). Suy ra một vectơ pháp tuyến của \(\left( {O'BC} \right)\) là \(\vec n = \left[ {\overrightarrow {BC} ,\overrightarrow {BO'} } \right] = \left( {2;6;3} \right)\). Mặt phẳng \(\left( {OBC} \right)\) có \(OO' \bot \left( {OBC} \right)\) nên \(\overrightarrow {OO'} = \left( {0;0;2} \right)\) là một vectơ pháp tuyến của \(\left( {OBC} \right)\). Suy ra \(\cos \left( {\left( {O'BC} \right),\left( {OBC} \right)} \right) = \left| {\cos \left( {\overrightarrow {OO'} ,\vec n} \right)} \right| = \frac{{\left| {2.0 + 6.0 + 3.2} \right|}}{{\sqrt {{2^2} + {6^2} + {3^2}} .\sqrt {{0^2} + {0^2} + {2^2}} }} = \frac{3}{7}\). Vậy \(\left( {\left( {O'BC} \right),\left( {OBC} \right)} \right) \approx {64^o}37'\). c) Ta có \(\overrightarrow {B'C} = \left( { - 3;1; - 2} \right)\) là một vectơ chỉ phương của đường thẳng \(B'C\). Ta có \(\vec n = \left( {2;6;3} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {O'BC} \right)\). Suy ra \(\sin \left( {B'C,\left( {O'BC} \right)} \right) = \left| {\cos \left( {\overrightarrow {B'C} ,\vec n} \right)} \right| = \frac{{\left| {\left( { - 3} \right).2 + 1.6 + \left( { - 2} \right).3} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{2^2} + {6^2} + {3^2}} }} = \frac{{3\sqrt {14} }}{{49}}\) Vậy \(\left( {B'C,\left( {O'BC} \right)} \right) \approx {13^o}15'\).
|