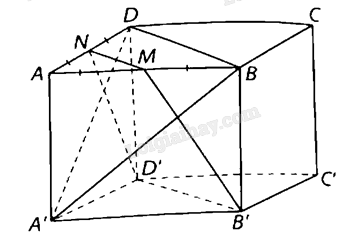
Giải bài 7.55 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sốngCho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\). Tổng hợp đề thi giữa kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\). a) Tính theo a thể tích khối chóp cụt \(AMN.A'B'D'\). b) Tính theo a khoảng cách giữa hai đường thẳng \(MN\) và \(A'B\). Phương pháp giải - Xem chi tiết a) Tính theo a thể tích khối chóp cụt \(AMN.A'B'D'\). Áp dụng công thức \(V = \frac{1}{3} \cdot AA' \cdot \left( {{S_{AMN}} + {S_{A'B'D'}} + \sqrt {{S_{AMN}} \cdot {S_{A'B'D'}}} } \right)\) b) Tính theo a khoảng cách giữa hai đường thẳng \(MN\) và \(A'B\).
Vậy \(d\left( {MN,A'B} \right) = d\left( {M,\left( {A'BD} \right)} \right) = \frac{{a\sqrt 3 }}{6}\). Lời giải chi tiết
a) Ta có: \({S_{A'B'D'}} = \frac{{{a^2}}}{2};{S_{AMN}} = \frac{{{a^2}}}{8};{S_{ABCD}} = {a^2};AA' = a\), suy ra thể tích khối chóp cụt \(AMN \cdot A'B'D'\) là: \(V = \frac{1}{3} \cdot AA' \cdot \left( {{S_{AMN}} + {S_{A'B'D'}} + \sqrt {{S_{AMN}} \cdot {S_{A'B'D'}}} } \right)\) \( = \frac{1}{3} \cdot a \cdot \left( {\frac{{{a^2}}}{8} + \frac{{{a^2}}}{2} + \sqrt {\frac{{{a^2}}}{8} \cdot \frac{{{a^2}}}{2}} } \right) = \frac{{7{a^3}}}{{24}}{\rm{.\;}}\) b) Vì \(MN//BD\) nên \(MN//\left( {A'BD} \right)\), do đó: \(d\left( {MN,A'B} \right) = d\left( {MN,\left( {A'BD} \right)} \right) = d\left( {M,\left( {A'BD} \right)} \right).\) Vì \(M\) là trung điểm của \(AB\) nên \(d\left( {M,\left( {A'BD} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A'BD} \right)} \right)\). Đặt \(h = d\left( {A,\left( {A'BD} \right)} \right)\) thì \(\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{A^{{\rm{'}}2}}}} = \frac{3}{{{a^2}}}\), suy ra \(h = \frac{{a\sqrt 3 }}{3}\). Vậy \(d\left( {MN,A'B} \right) = d\left( {M,\left( {A'BD} \right)} \right) = \frac{{a\sqrt 3 }}{6}\).
|