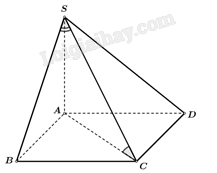
Giải bài 7.14 trang 30 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA \bot \left( {ABCD} \right)$, $SA = a\sqrt 2$.

a) Tính góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$.

b) Tính tang góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$.

Quảng cáo

Lời giải chi tiết

a) Ta có $SA \bot \left( {ABCD} \right) \Rightarrow AC$ là hình chiếu vuông góc của $SC$ lên mặt phẳng $\left( {ABCD} \right)$.

Khi đó $\left( {\widehat {SC,\left( {ABCD} \right)}} \right) = \left( {\widehat {SC,AC}} \right) = \widehat {SCA}$.

Mặt khác tam giác $SAC$ vuông tại $A$ có $AC = a\sqrt 2$ và $\tan \widehat {SCA} = \frac{{SA}}{{AC}} = 1 \Rightarrow \widehat {SCA} = 45^\circ$.

Vậy đường thẳng $SC$ hợp với mặt phẳng $\left( {ABCD} \right)$ một góc $45^\circ$.

b) Ta có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow SB$ là hình chiếu vuông góc của $SC$ lên mp$\left( {SAB} \right)$.

Khi đó $\left( {\widehat {SC,\left( {SAB} \right)}} \right) = \left( {\widehat {SC,SB}} \right) = \widehat {B{\rm{S}}C}$.

Mặt khác tam giác $SBC$ vuông tại $B$ có $BC = a,SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 3$.

Do đó $\tan \widehat {BSC} = \frac{{BC}}{{SB}} = \frac{{\sqrt 3 }}{3}$.

Vậy tang góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là $\frac{{\sqrt 3 }}{3}$.