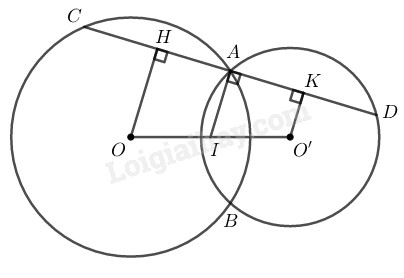
Bài 68 trang 168 SBT toán 9 tập 1Giải bài 68 trang 168 sách bài tập toán 9. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD. Đề bài Cho hai đường tròn (O) và (O′) cắt nhau tại A và B. Gọi I là trung điểm của OO′. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O′) tại C và D (khác A). Chứng minh rằng AC=AD. Phương pháp giải - Xem chi tiết Sử dụng kiến thức: +) Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau. +) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. Lời giải chi tiết
Kẻ OH⊥CD,O′K⊥CD Ta có: IA⊥CD Suy ra: OH//IA//O′K Theo giả thiết: IO=IO′ Suy ra: AH=AK (1) (tính chất đường thẳng song song cách đều) Xét đường tròn (O) có OH⊥AC mà OH là 1 phần đường kính và AC là dây cung Suy ra: HA=HC=12AC (quan hệ giữa đường kính và dây cung) ⇒AC=2AH(2) Xét đường tròn (O') có O′K⊥AD mà O'K là 1 phần đường kính và AD là dây cung Suy ra: KA=KD=12AD ( quan hệ giữa đường kính và dây cung) ⇒AD=2AK(3) Từ (1),(2) và (3) suy ra: AC=AD. xemloigiai.com
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
