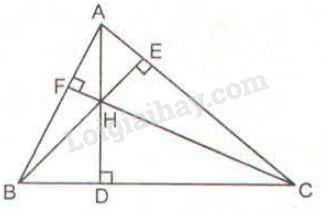
Bài 55 trang 98 SBT toán 8 tập 2Giải bài 55 trang 98 sách bài tập toán 8. Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH. Đề bài Tam giác ABC có ba đường cao AD,BE,CF đồng quy tại H. Chứng minh rằng AH.DH=BH.EH=CH.FH. Phương pháp giải - Xem chi tiết Sử dụng: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. Từ đó suy ra các hệ thức cần chứng minh. Lời giải chi tiết
Xét ∆ AFH và ∆ CDH có: +) \widehat {AFH} = \widehat {CDH} = 90^\circ +) \widehat {AHF} = \widehat {CHD} (đối đỉnh) \Rightarrow ∆ AFH đồng dạng ∆ CDH (g.g) \Rightarrow\displaystyle {{AH} \over {CH}} = {{FH} \over {DH}} \Rightarrow AH.DH = CH.FH (1) Xét ∆ AEH và ∆ BDH có: \widehat {AEH} = \widehat {BDH} = 90^\circ \widehat {AHE} = \widehat {BHD} (đối đỉnh) \Rightarrow ∆ AEH đồng dạng ∆ BDH (g.g) \Rightarrow\displaystyle{{AH} \over {BH}} = {{EH} \over {DH}} \Rightarrow AH.DH = BH.EH (2) Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH (đpcm). xemloigiai.com
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
