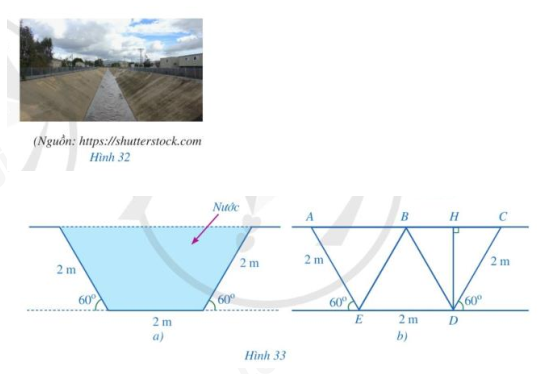
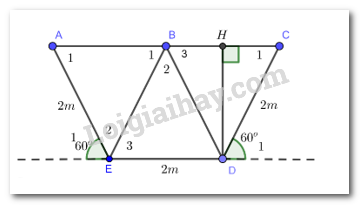
Giải bài 5 trang 104 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Hình 33a là mặt cắt đứng phần chứa nước của một con mương (hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC. H là hình chiếu của D trên đường thẳng BC.

a) Chứng minh rằng các tam giác BCD, BDE, ABE là các tam giác đều

b) Tính độ dài của DH, AC

c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước.

Lời giải chi tiết

a, Do ACDE là hình thang cân nên

AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)

Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)

Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung

\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)

Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.

Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.

Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.

Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.

b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.

Suy ra AC = AB + BC = 4m.

Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.

Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)

Xét \(\Delta DHC\) vuông tại H ta có:

\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)

\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)

c, Diện tích hình thang cân AEDC là:

\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)

Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)