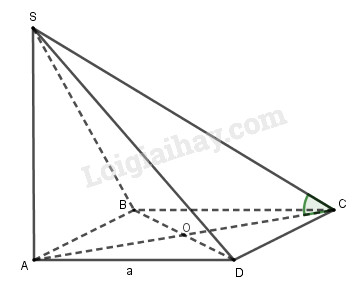
Bài 3.53 trang 163 SBT hình học 11

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD).

a) Chứng minh BD ⊥ SC.

b) Chứng minh (SAB) ⊥ (SBC).

c) Cho SA = (a√6)/3. Tính góc giữa SC và mặt phẳng (ABCD).

Quảng cáo

Lời giải chi tiết

a) Ta có: \(BD \bot AC\) (ABCD là hình vuông)

\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)

Do đó \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)

b) Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)

Mà \(BC \subset \left( {SBC} \right)\) nên \(\left( {SBC} \right) \bot \left( {SAB} \right)\).

c) Vì \(SA \bot \left( {ABCD} \right)\) nên A là hình chiếu của S trên (ABCD).

Mà \(SC \cap \left( {ABCD} \right) = C\) nên AC là hình chiếu của SC trên (ABCD)

Do đó góc giữa SC và (ABCD) bằng góc giữa SC và AC hay là góc \(\widehat {SCA}\).

Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)

Tam giác SAC vuông tại A nên \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} \) \(= \dfrac{{a\sqrt 6 }}{3}:a\sqrt 2 = \dfrac{{\sqrt 3 }}{3}\) \( \Rightarrow \widehat {SCA} = {30^0}\).

xemloigiai.com