Đề bài
Xem hình \(26\), hãy điền vào chỗ trống(...) để chứng minh định lí: " Hai góc đối đỉnh thì bằng nhau".
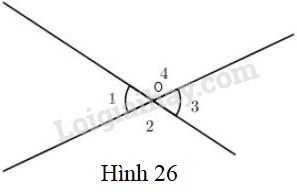
GT: ...
KL: ...
Các khẳng định | Căn cứ của khẳng định |
1 | \(\widehat{O_{1}}\) + \(\widehat{O_{2}}=180^0\) | Vì … |
2 | \(\widehat{O_{3}}\) + \(\widehat{O_{2}}\) = ... | Vì … |
3 | \(\widehat{O_{1}}\) + \(\widehat{O_{2}}\) = \(\widehat{O_{3}}\) + \(\widehat{O_{2}}\) | Căn cứ vào … |
4 | \(\widehat{O_{1}}\) = \(\widehat{O_{3}}\) | Căn cứ vào … |
Tương tự chứng minh \(\widehat{O_{2}} = \widehat{O_{4}}\)
- Hai góc đối đỉnh thì bằng nhau.
- Hai góc kề bù có tổng bằng \(180^0.\)
Lời giải chi tiết
GT: \(\widehat{O_{1}}\) đối đỉnh \(\widehat{O_{3}}\).
KL: \(\widehat{O_{1}} = \widehat{O_{3}}\)
Các khẳng định | Căn cứ của khẳng định |
1 | \(\widehat{O_{1}}\) + \(\widehat{O_{2}}=180^0\) | Vì \(\widehat{O_{1}}\) và \(\widehat{O_{2}}\) kề bù |
2 | \(\widehat{O_{3}}\) + \(\widehat{O_{2}}=180^0\) | Vì \(\widehat{O_{2}}\) và \(\widehat{O_{3}}\) kề bù |
3 | \(\widehat{O_{1}}\) + \(\widehat{O_{2}}\) = \(\widehat{O_{3}}\) + \(\widehat{O_{2}}\) | Căn cứ vào 1 và 2 |
4 | \(\widehat{O_{1}}\) = \(\widehat{O_{3}}\) | Căn cứ vào 3 |
Chứng minh \(\widehat{O_{2}} = \widehat{O_{4}}\)
Các khẳng định | Căn cứ của khẳng định |
1 | \(\widehat{O_{1}}\) + \(\widehat{O_{2}}=180^0\) | Vì \(\widehat{O_{1}}\) và \(\widehat{O_{2}}\) kề bù |
2 | \(\widehat{O_{1}}\) + \(\widehat{O_{4}}=180^0\) | Vì \(\widehat{O_{1}}\) và \(\widehat{O_{4}}\) kề bù |
3 | \(\widehat{O_{1}}\) + \(\widehat{O_{2}}\) = \(\widehat{O_{1}}\) + \(\widehat{O_{4}}\) | Căn cứ vào 1 và 2 |
4 | \(\widehat{O_{2}}\) = \(\widehat{O_{4}}\) | Căn cứ vào 3 |
xemloigiai.com














