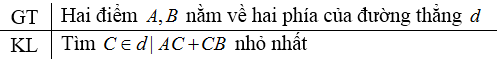Bài 24 trang 41 SBT toán 7 tập 2Giải bài 24 trang 41 sách bài tập toán 7. Cho hai điểm A và B nằm về hai phía của đường thẳng d. Tìm điểm C thuộc đường thẳng d sao cho tổng AC + CB là nhỏ nhất. Đề bài Cho hai điểm \(A\) và \(B\) nằm về hai phía của đường thẳng \(d. \) Tìm điểm \(C\) thuộc đường thẳng \(d\) sao cho tổng \(AC + CB\) là nhỏ nhất. Phương pháp giải - Xem chi tiết Sử dụng: Lời giải chi tiết
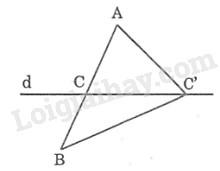
Gọi \(C\) là giao điểm của đoạn thẳng \(AB\) với đường thẳng \(d.\) Vì \(C \) nằm giữa \(A\) và \(B\) nên \(AC + CB = AB\) (1) Lấy điểm \(C’\) bất kỳ trên \(d\) \((C’\ne C)\) Nối \(AC’, BC’.\) Trong \(∆ABC’\) ta có: \(AC’ + BC’ > AB\) (bất đẳng thức tam giác) (2) Từ (1) và (2) suy ra: \(AC’ + C’B > AC + CB\) Vậy điểm \(C\) cần tìm là giao điểm của đoạn thẳng \(AB\) với đường thẳng \(d.\) xemloigiai.com
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
