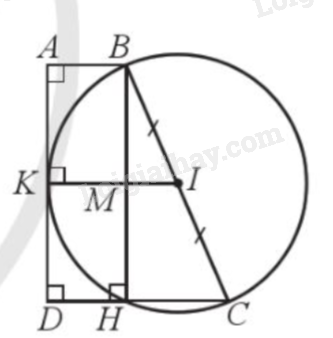
Giải bài 13 trang 106 sách bài tập toán 9 - Cánh diều tập 1

Đề bài

Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) có AB = 4 cm, BC = 13 cm, CD = 9 cm.

a) Tính độ dài đoạn thẳng AD.

b) Đường thẳng AD có tiếp xúc với đường tròn đường kính BC hay không? Vì sao?

Lời giải chi tiết

a) Kẻđường cao BH của hình thang ABCD.

Xét ABHD có \(\widehat A = \widehat D = \widehat {DHB} = 90^\circ \) nên ABHD là hình chữ nhật,

suy ra \(BH = AD\) và \(AB = DH = 4\)cm.

Ta lại có \(HC = DC - DH = 9 - 4 = 5\)cm.

Áp dụng định lý Pythagore trong tam giác BHC vuông tại H:

\(BH = \sqrt {B{C^2} - H{C^2}} = \sqrt {{{13}^2} - {5^2}} = 12\)cm.

Vậy \(BH = AD = 4\)cm.

b) Lấy I là trung điểm của BC, do đó I là tâm đường tròn đường kính BC và\(BI = R = \frac{{BC}}{2} = \frac{{13}}{2}\)cm.

Kẻ IK vuông góc với AD tại K, do đó IK = d là khoảng cách từ tâm I đến AD.

Xét HDKM có \(\widehat {MKD} = \widehat D = \widehat {MHD} = 90^\circ \) nên HDKM là hình chữ nhật, suy ra \(DH = KM = 4\)cm.

Ta có \(AD \bot DC;IK \bot AD\) nên \(IK//DC\). Mà \(M \in IK,H \in DC\) do đó \(MI//HC\).

Xét tam giác BHC có \(MI//HC\), I là trung điểm của BC nên MI là đường trung bình của tam giác BHC. Suy ra \(MI = \frac{{HC}}{2} = \frac{5}{2}\)cm.

Ta có \(IK = d = KM + MI = 4 + \frac{5}{2} = 6,5\)cm.

Do \(d = R\left( { = 6,5cm} \right)\) nên AD tiếp xúc với đường tròn đường kính BC.