Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 6Tổng hợp đề thi giữa kì 2 lớp 6 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN... Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?Đề bài I. Trắc nghiệm Câu 1 : Trong cách viết sau, cách viết nào cho ta phân số?
Câu 2 : Số đối của phân số \(\frac{5}{{ - 3}}\) là:
Câu 3 : Phân số \(\frac{{ - 6}}{{15}}\) bằng:
Câu 4 : Chọn kết quả đúng:
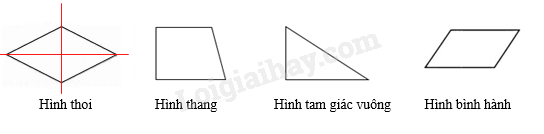
Câu 8 : Hình nào trong các hình sau vừa có trục đối xứng vừa có tâm đối xứng?
Câu 10 : Chọn câu đúng
II. Tự luận Lời giải và đáp án I. Trắc nghiệm Câu 1 : Trong cách viết sau, cách viết nào cho ta phân số?
Đáp án : C Phương pháp giải : Dựa vào khái niệm về phân số. Lời giải chi tiết : \(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\). \(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu. \(\frac{5}{{4,3}}\) không phải phân số vì \(4,3 \notin \mathbb{Z}\). \(\frac{{25}}{{ - 3}}\) là phân số vì \(25; - 3 \in \mathbb{Z}; - 3 \ne 0\). Đáp án C. Câu 2 : Số đối của phân số \(\frac{5}{{ - 3}}\) là:
Đáp án : A Phương pháp giải : Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\). Lời giải chi tiết : Số đối của phân số \(\frac{5}{{ - 3}}\) là\(\frac{5}{3}\). Đáp án A. Câu 3 : Phân số \(\frac{{ - 6}}{{15}}\) bằng:
Đáp án : B Phương pháp giải : Sử dụng quy tắc rút gọn phân số. Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có) Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm Lời giải chi tiết : Ta có: \(\frac{{ - 6}}{{15}} = \frac{{ - 6:3}}{{15:3}} = \frac{{ - 2}}{5}\). Đáp án B. Câu 4 : Chọn kết quả đúng:
Đáp án : A Phương pháp giải : Dựa vào quy tắc so sánh phân số Lời giải chi tiết : So sánh \(\frac{3}{{10}}\) với \(\frac{3}{7}\): \(\frac{3}{{10}} = \frac{{3.7}}{{10.7}} = \frac{{21}}{{70}}\); \(\frac{3}{7} = \frac{{3.10}}{{7.10}} = \frac{{30}}{{70}}\). Vì \(21 < 30\) nên \(\frac{{21}}{{70}} < \frac{{30}}{{70}}\). Do đó \(\frac{3}{{10}} < \frac{3}{7}\). Nên A đúng, B sai. \(\frac{8}{{15}} < \frac{9}{{15}} = \frac{3}{5}\) nên C sai. \(\frac{{ - 8}}{{10}} < 0 < \frac{3}{{74}}\) nên D sai. Đáp án A.
Đáp án : A Phương pháp giải : Dựa vào kiến thức về trục đối xứng. Lời giải chi tiết : Hình thoi có trục đối xứng.
Đáp án A.
Đáp án : B Phương pháp giải : Dựa vào kiến thức về tâm đối xứng. Lời giải chi tiết : Các biển có tâm đối xứng là biển hình 1, 3, 6.
Đáp án B.
Đáp án : D Phương pháp giải : Dựa vào kiến thức về trục đối xứng. Lời giải chi tiết : Các biển có trục đối xứng là biển 306, 405a, 401. Vậy biển 127 không có trục đối xứng.
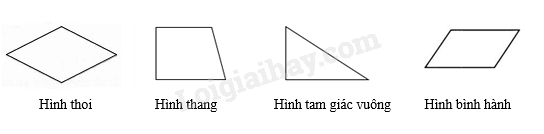
Đáp án D. Câu 8 : Hình nào trong các hình sau vừa có trục đối xứng vừa có tâm đối xứng?
Đáp án : A Phương pháp giải : Dựa vào kiến thức về trục đối xứng và tâm đối xứng. Lời giải chi tiết : Hình vuông vừa có trục đối xứng vừa có tâm đối xứng. Hình bình hành chỉ có tâm đối xứng không có trục đối xứng. Hình thang cân chỉ có trục đối xứng, không có tâm đối xứng. Hình tam giác cân chỉ có trục đối xứng, không có tâm đối xứng. Đáp án A.
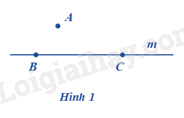
Đáp án : B Phương pháp giải : Quan sát hình vẽ để xác định. Lời giải chi tiết : Quan sát hình vẽ ta thấy điểm A không thuộc m, điểm B, C thuộc m nên ta có: \(A \notin m;b \in m;c \in m\). Vậy đáp án đúng là B. Đáp án B. Câu 10 : Chọn câu đúng
Đáp án : C Phương pháp giải : Dựa vào kiến thức về ba điểm thẳng hàng. Lời giải chi tiết : Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng nên C đúng. Đáp án C.
Đáp án : D Phương pháp giải : Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng. Lời giải chi tiết : Hình 1 và hình 3 biểu diễn điểm M là trung điểm của AB. Đáp án D.
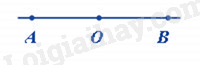
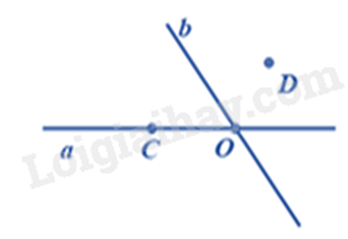
Đáp án : D Phương pháp giải : Dựa vào kiến thức về đoạn thẳng. Lời giải chi tiết : Hình vẽ có 3 đoạn thẳng, đó là: AO, OB, AB. Đáp án D. II. Tự luận Phương pháp giải : 1. Dựa vào quy tắc so sánh các phân số cùng tử số. 2. Sử dụng quy tắc tính với số thập phân để tìm x. Lời giải chi tiết : 1. Vì 2 < 4 < 5 < 6 nên \(\frac{1}{2} > \frac{1}{4} > \frac{1}{5} > \;\frac{1}{6}\) 2. a) \(x - \frac{3}{4} = \frac{{ - 2}}{3}\) \(\begin{array}{l}x = \frac{{ - 2}}{3} + \frac{3}{4}\\x = \frac{1}{{12}}\end{array}\) Vậy \(x = \frac{1}{{12}}\). b) \(\frac{{ - 3}}{4}:x + 1 = \frac{{ - 2}}{3}\) \(\begin{array}{l}\frac{{ - 3}}{4}:x = \frac{{ - 2}}{3} - 1\\\frac{{ - 3}}{4}:x = \frac{{ - 5}}{3}\\x = \frac{{ - 3}}{4}:\frac{{ - 5}}{3}\\x = \frac{9}{{20}}\end{array}\) Vậy \(x = \frac{9}{{20}}\). c) \(\frac{{x - 3}}{{12}} = \frac{{ - 5}}{4}\) \(\begin{array}{l}\left( {x - 3} \right).4 = - 5.12\\4\left( {x - 3} \right) = - 60\\x - 3 = - 60:4\\x - 3 = - 15\\x = - 15 + 3\\x = - 12\end{array}\) Vậy \(x = - 12\). Phương pháp giải : Dựa vào quy tắc tính với phân số. Lời giải chi tiết : a) \(\frac{{10}}{{11}} + \frac{3}{{11}}:3 - \frac{1}{7}\)\( = \frac{{10}}{{11}} + \frac{1}{{11}} - \frac{1}{7}\)\( = \frac{{11}}{{11}} - \frac{1}{7}\)\( = 1 - \frac{1}{7}\)\( = \frac{6}{7}\) b) \(\frac{{ - 3}}{7} + \frac{5}{{13}} + \frac{3}{7}\)\( = \left( {\frac{{ - 3}}{7} + \frac{3}{7}} \right) + \frac{5}{{13}}\)\( = 0 + \frac{5}{{13}}\)\( = \frac{5}{{13}}\) c) \(\frac{5}{3} \cdot \frac{7}{{25}} + \frac{5}{3} \cdot \frac{{21}}{{25}} - \frac{5}{3} \cdot \frac{7}{{25}}\)\( = \frac{5}{3}.\left( {\frac{7}{{25}} + \frac{{21}}{{25}} - \frac{7}{{25}}} \right)\)\( = \frac{5}{3}.\frac{{21}}{{25}}\)\( = \frac{7}{5}\) Phương pháp giải : Tính số táo cửa hàng bán được bằng tổng số táo . \(\frac{2}{3}\) Tính số táo còn lại bằng tổng số táo – số táo bán được. Lời giải chi tiết : Số táo cửa hàng bán được là: \(300.\frac{2}{3} = 200\) (kg) Số táo cửa hàng còn lại là: \(300 - 200 = 100\)(kg) Vậy số táo cửa hàng còn lại là 100kg. Phương pháp giải : 1. Quan sát hình vẽ để trả lời. 2. Sử dụng kiến thức về trung điểm của một đoạn thẳng. Lời giải chi tiết : 1. a) Điểm C, O thuộc đường thẳng a. b) Điểm O thuộc đường thẳng a và b. 2.
Ta có \(C\) nằm giữa \(A\) và \(B\) nên \(AC + BC = AB\) Hay \(BC = AB - AC = 7 - 3 = 4cm\). Vì \(M\) là trung điểm \(BC\) nên \(BM = \frac{{BC}}{2} = \frac{4}{2} = 2(cm)\). Vậy BM = 2cm. Phương pháp giải : Lấy 1 – A; 1 – B. So sánh 1 – A và 1 – B từ đó ta so sánh được A và B. Lời giải chi tiết : +) \(1 - A = 1 - \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2023}} + 1}}{{{{10}^{2023}} + 1}} - \frac{{{{10}^{2022}} + 1}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2023}} - {{10}^{2022}}}}{{{{10}^{2023}} + 1}} = \frac{{{{10}^{2022}}.9}}{{{{10}^{2023}} + 1}}\) +) \(1 - B = 1 - \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2022}} + 1}}{{{{10}^{2022}} + 1}} - \frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2022}} - {{10}^{2021}}}}{{{{10}^{2022}} + 1}} = \frac{{{{10}^{2021}}.9}}{{{{10}^{2022}} + 1}}\) +) Để so sánh \(1 - A\) và \(1 - B\) ta so sánh \(\frac{{10}}{{{{10}^{2023}} + 1}}\) và \(\frac{1}{{{{10}^{2022}} + 1}}\) \(\frac{1}{{{{10}^{2022}} + 1}} = \frac{{10}}{{{{10}^{2023}} + 10}} < \frac{{10}}{{{{10}^{2023}} + 1}}\) Suy ra \(1 - B < 1 - A\) Suy ra \(A < B\). Vậy A < B.
|