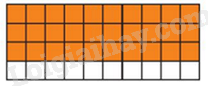
Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 10Tổng hợp đề thi giữa kì 2 lớp 6 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN... Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:Đề bài I. Trắc nghiệm
Câu 2 : Giá trị \(\frac{3}{4}\) của – 60 là:
Câu 3 : Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi
Câu 4 : Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?
Câu 7 : Trong tự nhiên, hình nào trong các hình dưới đây không có tâm đối xứng
Câu 8 : Chọn phát biểu sai. Khi O là trung điểm của đoạn AB thì
Câu 10 : Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là
Câu 11 : Em hãy chọn câu đúng.
II. Tự luận Lời giải và đáp án I. Trắc nghiệm
Đáp án : B Phương pháp giải : Quan sát hình vẽ và tìm các phân số bằng với phân số đó.. Lời giải chi tiết : Ta thấy trong hình có 40 ô và có 30 ô màu cam nên ta có phân số biểu diễn phần tô màu cam trong hình bên là \(\frac{{30}}{{40}}\). Các phân số bằng với phân số \(\frac{{30}}{{40}}\) là \(\frac{3}{4}\) và \(\frac{6}{8}\). Vậy phân số không biểu diễn là phân số \(\frac{1}{4}\). Đáp án B. Câu 2 : Giá trị \(\frac{3}{4}\) của – 60 là:
Đáp án : D Phương pháp giải : Tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\). Lời giải chi tiết : Giá trị \(\frac{3}{4}\) của – 60 là: \(\left( { - 60} \right).\frac{3}{4} = - 45\). Đáp án D. Câu 3 : Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi
Đáp án : B Phương pháp giải : Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi \(ad = bc\). Lời giải chi tiết : Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi\(a.4 = 3.b\). Đáp án B. Câu 4 : Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?
Đáp án : B Phương pháp giải : Sử dụng quy tắc rút gọn phân số. Lời giải chi tiết : \(\frac{{ - 27}}{{63}} = \frac{{ - 27:9}}{{63:9}} = \frac{{ - 3}}{7}\). Đáp án B.
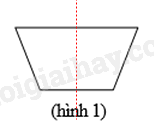
Đáp án : A Phương pháp giải : Dựa vào kiến thức về trục đối xứng. Lời giải chi tiết : Hình có trục đối xứng là hình 1.
Đáp án A.
Đáp án : D Phương pháp giải : Dựa vào kiến thức về trục đối xứng. Lời giải chi tiết : Cả ba công trình trên đều có trục đối xứng.
Đáp án D. Câu 7 : Trong tự nhiên, hình nào trong các hình dưới đây không có tâm đối xứng
Đáp án : B Phương pháp giải : Dựa vào kiến thức về tâm đối xứng. Lời giải chi tiết : Trong các hình này, hình không có tâm đối xứng là hình sao biển.
Đáp án B. Câu 8 : Chọn phát biểu sai. Khi O là trung điểm của đoạn AB thì
Đáp án : C Phương pháp giải : Dựa vào kiến thức về tính đối xứng. Lời giải chi tiết : O là trung điểm của AB thì A đối xứng với B qua O nên A đúng C sai. O đối xứng với O qua chính nó nên B đúng. Đáp án C.
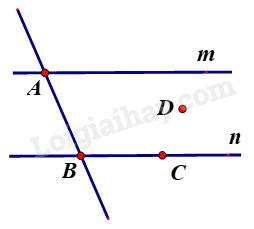
Đáp án : B Phương pháp giải : Quan sát hình vẽ để trả lời. Lời giải chi tiết : Đường thẳng n đi qua điểm B và điểm C Đáp án B. Câu 10 : Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là
Đáp án : C Phương pháp giải : Dựa vào kiến thức về tia đối. Lời giải chi tiết : Tia đối của tia FQ là tia FP (vì F nằm giữa P và Q). Đáp án C. Câu 11 : Em hãy chọn câu đúng.
Đáp án : B Phương pháp giải : Dựa vào kiến thức về đường thẳng. Lời giải chi tiết : Qua hai điểm phân biệt chỉ có 1 đường thẳng nên A sai. Có vô số điểm cùng thuộc một đường thẳng. nên B đúng. Hai đường thẳng phân biết chưa chắc đã song song nên C sai. Trong ba điểm thẳng hàng chỉ có một điểm nằm giữa nên D sai. Đáp án B.
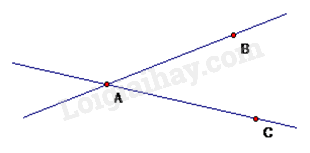
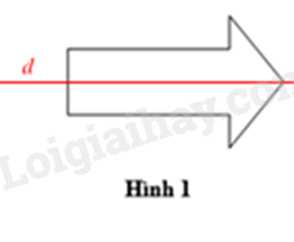
Đáp án : A Phương pháp giải : Quan sát hình vẽ để xác định. Lời giải chi tiết : Hai đường thẳng AB và AC cắt nhau tại A. Đáp án A. II. Tự luận Phương pháp giải : Dựa vào quy tắc tính với phân số. Lời giải chi tiết : a) \(\frac{{ - 3}}{7} + \frac{5}{7} = \frac{2}{7}\) b) \(\frac{2}{3} + \frac{{ - 3}}{5} = \frac{{10}}{{15}} + \frac{{ - 9}}{{15}} = \frac{1}{{15}}\) c) \(\frac{2}{9} - \left( {\frac{1}{{20}} + \frac{2}{9}} \right) = \frac{2}{9} - \frac{1}{{20}} - \frac{2}{9} = - \frac{1}{{20}}\) d) \(\frac{{11}}{{23}}.\frac{{12}}{{17}} + \frac{{11}}{{23}}.\frac{5}{{17}} + \frac{{12}}{{23}}\)\( = \frac{{11}}{{23}}.\left( {\frac{{12}}{{17}} + \frac{5}{{17}}} \right) + \frac{{12}}{{23}}\) \( = \frac{{11}}{{23}} \cdot 1 + \frac{{12}}{{23}}\)\( = \frac{{23}}{{23}}\)\( = 1\) Phương pháp giải : Dựa vào kiến thức về trục đối xứng, tâm đối xứng để xác định. Lời giải chi tiết : a) Ta vẽ được đường thẳng d là trục đối xứng của Hình 1 như sau:
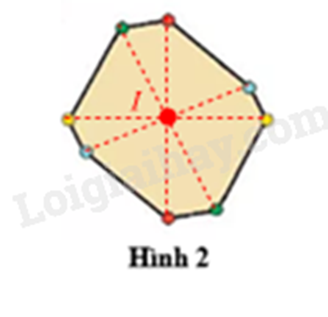
b) Tâm đối xứng I của hình 2 là giao điểm của các đoạn thẳng nối các chấm cùng màu.
Phương pháp giải : Áp dụng cách tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\). Lời giải chi tiết : Số gạo còn lại sau ngày thứ nhất bán tương ứng với phân số \(1 - {1 - \frac{1}{3}} = \frac{2}{3}\) (tổng số gạo) Khi đó số gạo ngày thứ hai bán được là: \(\frac{4}{9}.\frac{2}{3} = \frac{8}{{27}}\) (tổng số gạo) 1400kg gạo tương ứng với phân số \(1 - \frac{1}{3} - \frac{8}{{27}} = \frac{{10}}{{27}}\) (tổng số gạo). Do đó số gạo bán được trong 3 ngày là: \(1400:\frac{{10}}{{27}} = 3780\) (kg) Vậy số gạo bán được trong cả ba ngày là 3780kg. Phương pháp giải : Vẽ hình theo yêu cầu. a) Chứng minh OA < OB nên A nằm giữa O và B. b) Tính KA dựa vào KO và OA. So sánh KA và AB. Lời giải chi tiết :
a) Trên tia Ox ta có OA = 3cm, OB = 6cm vì 3 < 6 nên OA < OB Do đó A nằm giữa O và B. (1) Suy ra: OA + AB = OB Thay số ta được 3 + AB = 6 Suy ra AB = 3(cm) Mà OA = 3(cm) nên OA = AB (2) Từ (1) và (2) suy ra: A là trung điểm của OB (đpcm) b) Ta có A thuộc tia Ox, K thuộc tia đối của tia Ox nên A và K nằm khác phía đối với O hay O nằm giữa K và A. Suy ra KO + OA = KA. Thay số ta được 1 + 3 = KA Suy ra KA = 4(cm). Mà AB = 3cm nên KA > AB (do 4 > 3). Vậy KA > AB. Phương pháp giải : Tính chiều rộng của mảnh vườn theo chiều dài. Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích mảnh vườn. Lời giải chi tiết : Chiều rộng của mảnh vườn là: \(10.\frac{3}{5} = 6\left( m \right)\) Diện tích của mảnh vườn là: \(10.6 = 60\left( {{m^2}} \right)\) Vậy diện tích mảnh vườn là \(60{m^2}\).
|