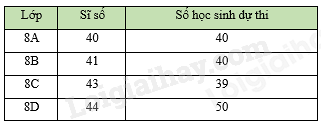
Đề thi giữa kì 2 Toán 8 - Đề số 5 - Cánh diềuTổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Câu 1 (150791): Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:Đề bài I. Trắc nghiệm Câu 1 : Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
Câu 2 : Bạn An đứng ở cổng trường và ghi lại xem bạn nào ra về bằng xe đạp khi tan trường. Phương pháp thu thập dữ liệu của bạn An là
Câu 3 : Nhiệt độ trung bình của các tháng trong năm của một quốc gia được biểu diễn trong bảng sau:
Biểu đồ thích hợp để biểu diễn trong bảng trên là
Câu 4 : Một hộp chứa 10 tấm thẻ cùng loại được đánh từ 4 đến 13. An lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số nguyên tố là:
Câu 5 : Gieo một con xúc xắc cân đối và đồng chất. Xác suất của biến cố “Gieo được mặt có số chấm lẻ” là:
Câu 6 : Lớp 8A có 40 học sinh, trong đó có 22 nam và 18 nữ. Gặp ngẫu nhiên một học sinh của lớp, xác suất của biến cố “Học sinh đó nữ” là:
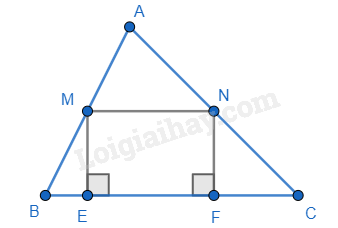
Câu 7 : Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
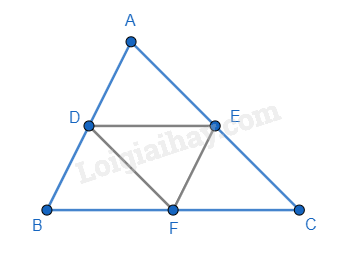
Câu 8 : Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là:
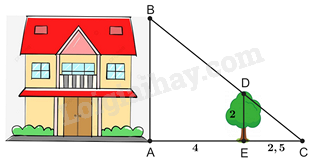
Câu 10 : Để tính chiều cao AB của ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 2m và biết được các khoảng cách AE = 4m, EC = 2,5m.
Khi đó chiều cao AB của ngôi nhà là:
II. Tự luận Lời giải và đáp án I. Trắc nghiệm Câu 1 : Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
Đáp án : D Phương pháp giải : Quan sát bảng thống kê để chỉ ra dữ liệu chưa hợp lý Lời giải chi tiết : Quan sát bảng thống kê, ta thấy lớp 8D có sĩ số 44 học sinh nhưng số học sinh dự thi là 50 > 44 không hợp lí. Câu 2 : Bạn An đứng ở cổng trường và ghi lại xem bạn nào ra về bằng xe đạp khi tan trường. Phương pháp thu thập dữ liệu của bạn An là
Đáp án : B Phương pháp giải : Dựa vào kiến thức về các phương pháp thu thập dữ liệu. Lời giải chi tiết : Phương pháp thu thập dữ liệu của bạn An là từ nguồn quan sát. Câu 3 : Nhiệt độ trung bình của các tháng trong năm của một quốc gia được biểu diễn trong bảng sau:
Biểu đồ thích hợp để biểu diễn trong bảng trên là
Đáp án : B Phương pháp giải : Dựa vào kiến thức về biểu đồ. Lời giải chi tiết : Biểu đồ thích hợp để biểu diễn trong bảng trên là biểu đồ đoạn thẳng. Câu 4 : Một hộp chứa 10 tấm thẻ cùng loại được đánh từ 4 đến 13. An lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số nguyên tố là:
Đáp án : C Phương pháp giải : Liệt kê các kết quả thuận lợi để tính xác suất. Lời giải chi tiết : Có 4 tấm thẻ ghi số nguyên tố là: 5; 7; 11; 13. Xác suất để thẻ chọn ra ghi số nguyên tố là: \(\frac{4}{{10}} = 0,4\). Câu 5 : Gieo một con xúc xắc cân đối và đồng chất. Xác suất của biến cố “Gieo được mặt có số chấm lẻ” là:
Đáp án : A Phương pháp giải : Liệt kê các kết quả thuận lợi cho biến cố để tính xác suất. Lời giải chi tiết : Có 3 kết quả thuận lợi cho biến cố “Gieo được mặt có số chấm lẻ” là: 1; 3; 5. Xác suất của biến cố “Gieo được mặt có số chấm lẻ” là: \(\frac{3}{6} = \frac{1}{2}\). Câu 6 : Lớp 8A có 40 học sinh, trong đó có 22 nam và 18 nữ. Gặp ngẫu nhiên một học sinh của lớp, xác suất của biến cố “Học sinh đó nữ” là:
Đáp án : A Phương pháp giải : Xác suất của biến cố “Học sinh đó nữ” bằng tỉ số giữa số học sinh nữ với tổng số học sinh. Lời giải chi tiết : Xác suất của biến cố “Học sinh đó nữ” là: \(\frac{{18}}{{40}} = \frac{9}{{20}} = 0,45\). Câu 7 : Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
Đáp án : C Phương pháp giải : Dựa vào kiến thức về đường trung bình trong tam giác và dấu hiệu nhận biết hình học. Lời giải chi tiết :
Ta có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC nên MN // BC và MN = \(\frac{1}{2}\)BC. => MN // EF (E,F \( \in \) BC) nên A đúng. Ta có ME \( \bot \) BC, NF \( \bot \) BC => ME // NF. Tứ giác MNFE có MN // EF (E,F \( \in \) BC); ME // NF nên MNFE là hình bình hành. => MN = EF; ME = NF (cặp cạnh tương ứng) nên B và D đúng. MN = ME không có đủ điều kiện để xác định nên C sai. Câu 8 : Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là:
Đáp án : A Phương pháp giải : Sử dụng tính chất của đường trung bình để tính. Lời giải chi tiết :
Ta có D, E, F là trung điểm của các cạnh AB, AC, BC nên DE, EF và DF là đường trung bình của tam giác ABC nên \(DE = \frac{1}{2}BC;EF = \frac{1}{2}AB;DF = \frac{1}{2}AC\). Suy ra chu vi tam giác DEF là: DE + EF + DF = \(\frac{1}{2}\)BC + \(\frac{1}{2}\)AB + \(\frac{1}{2}\)AC = \(\frac{1}{2}\)(BC + AB + AC) = \(\frac{1}{2}\).80 = 40(cm).
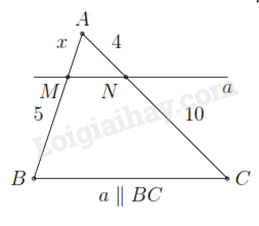
Đáp án : C Phương pháp giải : Sử dụng định lí Thales. Lời giải chi tiết : Do a // BC, áp dụng định lí Thales ta có: \(\begin{array}{l}\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\\\frac{x}{5} = \frac{4}{{10}}\\x = 2\end{array}\) Câu 10 : Để tính chiều cao AB của ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 2m và biết được các khoảng cách AE = 4m, EC = 2,5m.
Khi đó chiều cao AB của ngôi nhà là:
Đáp án : A Phương pháp giải : Áp dụng hệ quả của định lí Thales trong tam giác để tính AB. Lời giải chi tiết : Vì ngôi nhà và cái cây cùng vuông góc với mặt đất nên chúng song song với nhau \( \Rightarrow AB//DE\). Xét tam giác ABC có \(AB//DE\) nên ta có: \(\frac{{AB}}{{AC}} = \frac{{DE}}{{EC}}\) (hệ quả của định lí Thales) \( \Rightarrow AB = \frac{{DE}}{{EC}}.AC = \frac{2}{{2,5}}.\left( {4 + 2,5} \right) = 5,2\left( m \right)\)
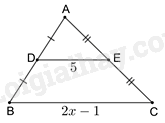
Đáp án : A Phương pháp giải : Áp dụng tính chất của đường trung bình trong tam giác. Lời giải chi tiết : Xét tam giác ABC có: D là trung điểm của AB (AD = DB) E là trung điểm của AC (AE = EC) \( \Rightarrow DE\) là đường trung bình của tam giác ABC. \(\begin{array}{l} \Rightarrow DE = \frac{1}{2}\left( {2x - 1} \right)\\5 = x - \frac{1}{2}\\x = 5,5\end{array}\)
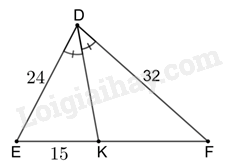
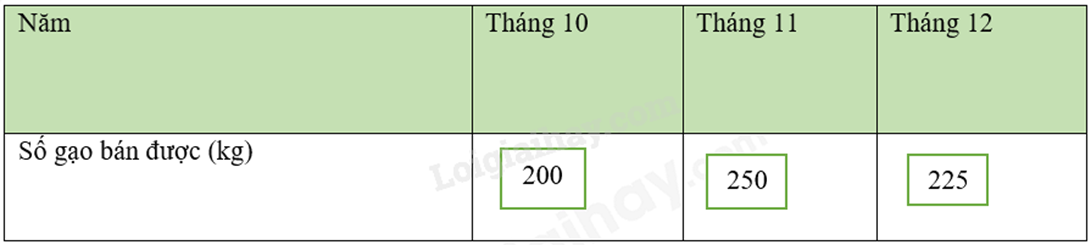
Đáp án : A Phương pháp giải : Dựa vào tính chất tia phân giác trong tam giác. Lời giải chi tiết : Ta có DK là tia phân giác của góc EDF nên \(\frac{{DE}}{{EK}} = \frac{{DF}}{{KF}} \Rightarrow KF = DF:\frac{{DE}}{{EK}} = 32:\frac{{24}}{{15}} = 20\). II. Tự luận Phương pháp giải : Liệt kê các kết quả có thể xảy ra. Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả. Lời giải chi tiết : Có 6 kết quả có thể xảy ra khi lấy ngẫu nhiên 2 viên bi từ túi là: (X – Đ); (X – T); (X – V); (Đ – T); (Đ – V); (T – V). Có 3 kết quả thuận lợi cho biến cố A là: (X – Đ); (Đ – T); (Đ – V). Xác suất của biến cố A là: \(\frac{3}{6} = \frac{1}{2}\). Có 3 kết quả thuận lợi cho biến cố B là: (X – Đ); (X – V); (Đ – V). Xác suất của biến cố B là: \(\frac{3}{6} = \frac{1}{2}\). Phương pháp giải : a) Dựa vào dữ liệu đề bài cho để điền vào bảng. b) Điền số tương ứng vào biểu đồ. Lời giải chi tiết : a)
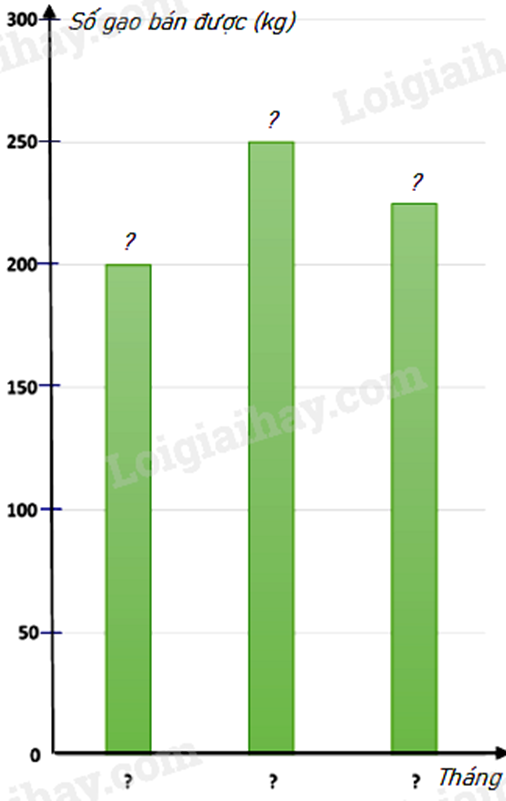
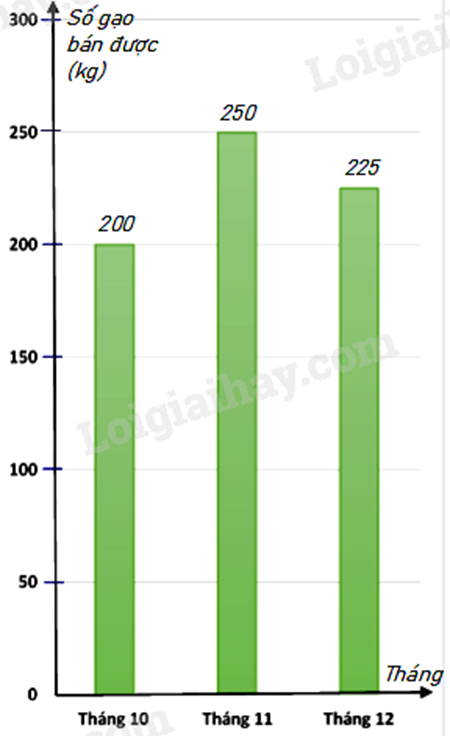
b) Biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh là :
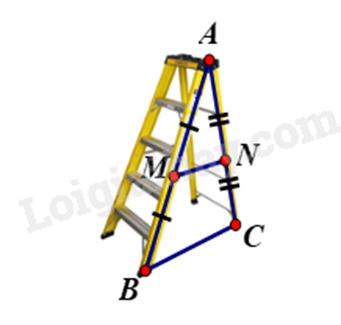
Phương pháp giải : Dựa vào tính chất của đường trung bình để tính. Lời giải chi tiết :
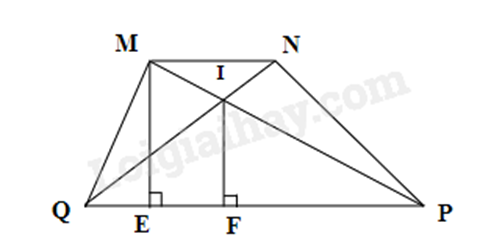
Gọi MN là thanh ngang; BC là độ rộng giữa hai bên thang. MN nằm chính giữa thang nên M; N là trung điểm AB và AC. Suy ra MN là đường trung bình của tam giác ABC. Suy ra MN = \(\frac{1}{2}BC = \frac{1}{2}.80 = 40\,\,(cm)\). Vậy người thợ đã làm thanh ngang đó dài 40 cm. Phương pháp giải : a) Sử dụng công thức tính diện tích hình thang để suy ra đường cao ME. b) Sử dụng hệ quả của định lí Thales để chứng minh. c) Sử dụng hệ quả của định lí Thales để tính IF. Sử dụng công thức tính diện tích tam giác. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}{S_{MNPQ}} = \frac{1}{2}\left( {MN + PQ} \right).ME\\ \Rightarrow ME = \frac{{2{S_{MNPQ}}}}{{MN + PQ}} = \frac{{2.36}}{{4 + 8}} = 6\left( {cm} \right)\end{array}\) b) Xét \(\Delta IPQ\) có MN // PQ nên \(\frac{{IP}}{{IM}} = \frac{{PQ}}{{MN}} \Rightarrow \frac{{IP}}{{IM}} = \frac{8}{4} = 2\) (hệ quả của định lí Thales) \(\begin{array}{l} \Rightarrow \frac{{IP}}{{IP + IM}} = \frac{2}{{2 + 1}}\\ \Rightarrow \frac{{IP}}{{MP}} = \frac{2}{3}\end{array}\) \( \Rightarrow IP = \frac{2}{3}MP\) (đpcm) c) Kẻ \(IF \bot PQ\), mà \(ME \bot PQ\) \( \Rightarrow IF//ME\) Do \(\Delta PME\) có \(IF//ME\) nên \(\frac{{IF}}{{ME}} = \frac{{IP}}{{MP}} = \frac{2}{3}\) \( \Rightarrow IF = \frac{2}{3}ME \Rightarrow IF = \frac{2}{3}.6 = 4\left( {cm} \right)\) \( \Rightarrow {S_{\Delta IPQ}} = \frac{{IF.PQ}}{2} = \frac{{4.8}}{2} = 16\left( {c{m^2}} \right)\) Phương pháp giải : Tìm điều kiện để hai đường thẳng cắt nhau. Tìm tọa độ giao điểm 2 đường thẳng. Tìm nghiệm nguyên. Lời giải chi tiết : Ta có: \(d \cap d'\) khi và chỉ khi \(m \ne 2\). Xét phương trình hoành độ giao điểm của hai đường thẳng d và d’, ta có: \(\begin{array}{l}mx - 2 = 2x + 1\\mx - 2x = 1 + 2\\\left( {m - 2} \right)x = 3\\x = \frac{3}{{m - 2}}\end{array}\) Để hai đường thẳng d và d’ cắt nhau tại điểm có hoành độ là số nguyên thì \(x = \frac{3}{{m - 2}} \in \mathbb{Z}\) \( \Leftrightarrow 3 \vdots \left( {m - 2} \right)\) hay \(m - 3 \in \) Ư(3) \( = \left\{ { \pm 1; \pm 3} \right\}\). Ta có bảng giá trị sau:
Vậy \(m \in \left\{ { - 1;1;3;5} \right\}\) thì hai đường thẳng d: y = mx -2; d’: y = 2x + 1 cắt nhau tại điểm có hoành độ là số nguyên.
|