Đề thi giữa kì 2 Toán 8 - Đề số 3 - Kết nối tri thứcĐã có lời giải SGK Toán lớp 9 - Kết nối tri thức (mới) Đầy đủ - Chi tiết - Chính xác Đề bài I. Trắc nghiệm Khoanh tròn trước câu trả lời đúng. Câu 1 : Phân thức đối của phân thức \(\frac{3}{{x + 1}}\) là:
Câu 2 : Biểu thức \(A = \frac{2}{{x + 3}} + \frac{3}{{x + 1}}\) xác định khi:
Câu 3 : Rút gọn phân thức \(\frac{{3xy + 3}}{{9y + 3}}\) ta được:
Câu 4 : Giá trị của x để phân thức \(\frac{{5x - 2}}{{{x^2} + 2x + 1}} = 0\) là:
Câu 5 : Kết quả phép tính \(\left( {\frac{{ - 20x}}{{3{y^2}}}} \right):\left( { - \frac{{4{x^3}}}{{5y}}} \right)\) là
Câu 7 : Cho tam giác ABC vuông tại A, tính cạnh BC nếu biết \(\frac{{AB}}{3} = \frac{{AC}}{4}\) và \(AB + AC = 14cm\)
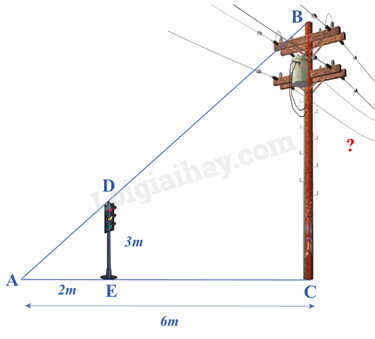
Câu 8 : Bóng của một cột điện trên mặt đất dài 6m. Cùng lúc đó, một cột đèn giao thông cao 3m có bóng dài 2m. Tính chiều cao của cột điện.
II. Tự luận Câu 1 : Cho biểu thức \(M = \left( {\frac{1}{{x - 2}} - \frac{1}{{x + 2}}} \right):\frac{2}{{x + 2}}\) a) Tìm điều kiện xác định của M. b) Rút gọn M. c) Tìm x để \(M = 1\). Câu 2 : Tùng đạp xe từ nhà tới câu lạc bộ bóng đá dài 5km với tốc độ x (km/h). Lượt về thuận chiều gió nên vận tốc nhanh hơn lượt đi 3km/h. a) Viết biểu thức biểu thị tổng thời gian cả hai lượt đi và về. (kí hiệu là T) b) Viết biểu thức biểu thị hiệu thời gian lượt đi đối với lượt về. (kí hiệu là t) c) Tính T và t với x = 12. Câu 3 : Một cột đèn cao 10m chiếu sáng một cây xanh như hình dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét)
Câu 4 : Cho tam giác ABC vuông tại A (AB > AC). Gọi I là trung điểm của AB. Kẻ IN vuông góc với BC tại N (N thuộc BC). a) Chứng minh $\Delta ACB\backsim \Delta NIB$. Từ đó suy ra \(BA.BI = BC.BN\). b) Giả sử AC = 6cm, BC = 10cm. Tính BN. c) Chứng minh \(\widehat {IAN} = \widehat {ICN}\). d) Chứng minh \(A{C^2} = N{C^2} - N{B^2}\). Câu 5 : Chứng minh rằng nếu a, b, c khác nhau đôi một thì: \(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\). Lời giải và đáp án I. Trắc nghiệm Khoanh tròn trước câu trả lời đúng. Câu 1 : Phân thức đối của phân thức \(\frac{3}{{x + 1}}\) là:
Đáp án : A Phương pháp giải : Phân thức đối của phân thức \(\frac{A}{B}\) là \( - \frac{A}{B}\). Lời giải chi tiết : Phân thức đối của phân thức \(\frac{3}{{x + 1}}\) là \( - \frac{3}{{x + 1}}\). Câu 2 : Biểu thức \(A = \frac{2}{{x + 3}} + \frac{3}{{x + 1}}\) xác định khi:
Đáp án : A Phương pháp giải : Để phân thức xác định thì mẫu thức khác 0. Lời giải chi tiết : Phân thức \(\frac{2}{{x + 3}}\) xác định khi \(x + 3 \ne 0\) hay \(x \ne - 3\). Phân thức \(\frac{3}{{x + 1}}\) xác định khi \(x + 1 \ne 0\) hay \(x \ne - 1\). \( \Rightarrow \) Biểu thức A xác định khi \(x \ne - 3,x \ne - 1\). Câu 3 : Rút gọn phân thức \(\frac{{3xy + 3}}{{9y + 3}}\) ta được:
Đáp án : C Phương pháp giải : Thực hiện rút gọn phân thức theo 2 bước: + Bước 1: Phân tích tử và mẫu thành nhân tử (nếu cần). + Bước 2: Tìm nhân tử chung của tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó. Lời giải chi tiết : Ta có: \(\frac{{3xy + 3}}{{9y + 3}} = \frac{{3\left( {xy + 1} \right)}}{{3\left( {3y + 1} \right)}} = \frac{{xy + 1}}{{3y + 1}}\). Câu 4 : Giá trị của x để phân thức \(\frac{{5x - 2}}{{{x^2} + 2x + 1}} = 0\) là:
Đáp án : B Phương pháp giải : Biến đổi phân thức để tìm x. Lời giải chi tiết : Để phân thức \(\frac{{5x - 2}}{{{x^2} + 2x + 1}}\) xác định thì \({x^2} + 2x + 1 = {\left( {x + 1} \right)^2} \ne 0 \Rightarrow x \ne - 1\) Ta có: \(\begin{array}{l}\frac{{5x - 2}}{{{x^2} + 2x + 1}} = 0\\5x - 2 = 0\\x = \frac{2}{5}\left( {TM} \right)\end{array}\) Câu 5 : Kết quả phép tính \(\left( {\frac{{ - 20x}}{{3{y^2}}}} \right):\left( { - \frac{{4{x^3}}}{{5y}}} \right)\) là
Đáp án : A Phương pháp giải : Sử dụng quy tắc chia hai phân thức. Lời giải chi tiết : Ta có: \(\left( {\frac{{ - 20x}}{{3{y^2}}}} \right):\left( { - \frac{{4{x^3}}}{{5y}}} \right) = \frac{{ - 4.5x}}{{3{y^2}}}.\frac{{ - 5y}}{{4{x^3}}} = \frac{{25}}{{3{x^2}y}}\).
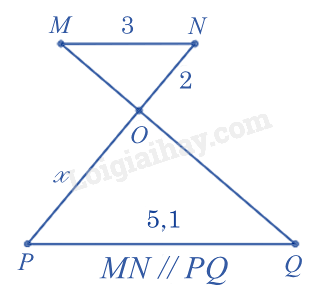
Đáp án : D Phương pháp giải : Dựa vào định lí hai tam giác đồng dạng. Lời giải chi tiết : Ta có: MN // PQ nên $\Delta OMN\backsim \Delta OQP$ (định lí hai tam giác đồng dạng) \( \Rightarrow \frac{{ON}}{{OP}} = \frac{{MN}}{{PQ}} \Rightarrow \frac{2}{x} = \frac{3}{{5,1}} \Rightarrow x = 2:\frac{3}{{5,1}} = 3,4\). Câu 7 : Cho tam giác ABC vuông tại A, tính cạnh BC nếu biết \(\frac{{AB}}{3} = \frac{{AC}}{4}\) và \(AB + AC = 14cm\)
Đáp án : D Phương pháp giải : Áp dụng tính chất dãy tỉ số bằng nhau để tính AB, AC. Áp dụng định lí Pythagore để tính BC. Lời giải chi tiết : Ta có: Áp dụng tính chất dãy tỉ số bằng nhau, ta có: \(\frac{{AB}}{3} = \frac{{AC}}{4} = \frac{{AB + AC}}{{3 + 4}} = \frac{{14}}{7} = 2\) \( \Rightarrow AB = 2.3 = 6\left( {cm} \right);AC = 2.4 = 8\left( {cm} \right)\). Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) \( \Rightarrow BC = 10cm\). Câu 8 : Bóng của một cột điện trên mặt đất dài 6m. Cùng lúc đó, một cột đèn giao thông cao 3m có bóng dài 2m. Tính chiều cao của cột điện.
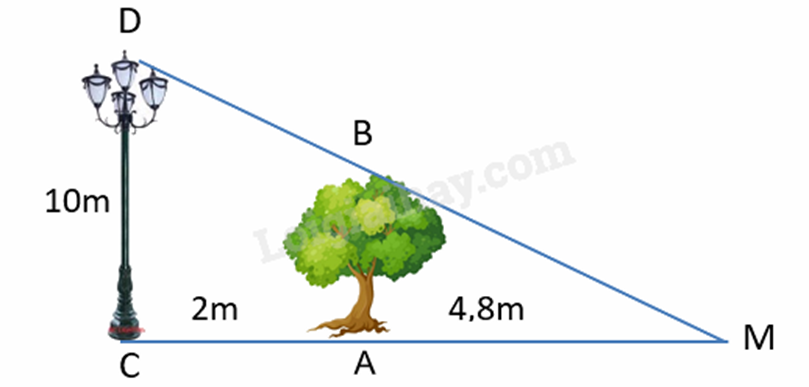
Đáp án : C Phương pháp giải : Sử dụng các trường hợp đồng dạng của tam giác vuông. Lời giải chi tiết : Vì cột đèn giao thông và cột điện vuông góc với mặt đất nên \(\widehat E = \widehat C = {90^0}\). Xét \(\Delta ADE\) và \(\Delta ABC\) có: \(\widehat E = \widehat C\left( { = {{90}^0}} \right)\) \(\widehat A\) chung $\Rightarrow \Delta ADE\backsim \Delta ABC\left( g.g \right)$ \( \Rightarrow \frac{{DE}}{{AE}} = \frac{{BC}}{{AC}}\) \(\frac{3}{2} = \frac{{BC}}{6} \Rightarrow BC = 6.\frac{3}{2} = 9\left( m \right)\). II. Tự luận Câu 1 : Cho biểu thức \(M = \left( {\frac{1}{{x - 2}} - \frac{1}{{x + 2}}} \right):\frac{2}{{x + 2}}\) a) Tìm điều kiện xác định của M. b) Rút gọn M. c) Tìm x để \(M = 1\). Phương pháp giải : a) Tìm điều kiện cho từng phân thức trong M. b) Sử dụng các phép tính để rút gọn M c) Thay M = 1 để tìm x. Lời giải chi tiết : a) Để M xác định thì: \(\left\{ \begin{array}{l}x - 2 \ne 0\\x + 2 \ne 0\end{array} \right.\) hay \(x \ne \pm 2\) b) Ta có: \(M = \left( {\frac{1}{{x - 2}} - \frac{1}{{x + 2}}} \right):\frac{2}{{x + 2}}\) \(\begin{array}{l}M = \left( {\frac{1}{{x - 2}} - \frac{1}{{x + 2}}} \right).\frac{{x + 2}}{2}\\M = \frac{1}{{x - 2}}.\frac{{x + 2}}{2} - \frac{1}{{x + 2}}.\frac{{x + 2}}{2}\\M = \frac{{x + 2}}{{2\left( {x - 2} \right)}} - \frac{1}{2}\\M = \frac{{x + 2 - \left( {x - 2} \right)}}{{2\left( {x - 2} \right)}}\\M = \frac{{x + 2 - x + 2}}{{2\left( {x - 2} \right)}}\\M = \frac{4}{{2\left( {x - 2} \right)}}\\M = \frac{2}{{x - 2}}\end{array}\) Vậy \(M = \frac{2}{{x - 2}}\). c) Thay M = 1, ta được: \(\begin{array}{l}\frac{2}{{x - 2}} = 1\\x - 2 = 2\\x = 4\end{array}\) Vậy x = 4 thì M = 1. Câu 2 : Tùng đạp xe từ nhà tới câu lạc bộ bóng đá dài 5km với tốc độ x (km/h). Lượt về thuận chiều gió nên vận tốc nhanh hơn lượt đi 3km/h. a) Viết biểu thức biểu thị tổng thời gian cả hai lượt đi và về. (kí hiệu là T) b) Viết biểu thức biểu thị hiệu thời gian lượt đi đối với lượt về. (kí hiệu là t) c) Tính T và t với x = 12. Phương pháp giải : Viết phân thức biểu thị thời gian của lượt đi, biểu thức biểu thị thời gian lượt về theo công thức: \(t = \frac{S}{v}\). a,b) Từ hai phân thức trên biết biểu thức biểu thị tổng và hiệu. c) Thay x = 12 vào T và t để tính. Lời giải chi tiết : Phân thức biểu thị thời gian của lượt đi là: \(\frac{5}{x}\) (giờ) Phân thức biểu thị thời gian của lượt về là: \(\frac{5}{{x + 3}}\) (giờ) a) Biểu thức biểu thị tổng thời gian cả hai lượt đi và về là: \(T = \frac{5}{x} + \frac{5}{{x + 3}}\) (giờ) b) Biểu thức biểu thị hiệu thời gian lượt đi đối với lượt về là: \(t = \frac{5}{x} - \frac{5}{{x + 3}}\) (giờ) c) Thay x = 12 vào biểu thức T và t, ta được: \(T = \frac{5}{{12}} + \frac{5}{{12 + 3}} = \frac{5}{{12}} + \frac{5}{{15}} = \frac{3}{4}\) (giờ) \(t = \frac{5}{{12}} - \frac{5}{{12 + 3}} = \frac{5}{{12}} - \frac{5}{{15}} = \frac{1}{{12}}\) (giờ) Câu 3 : Một cột đèn cao 10m chiếu sáng một cây xanh như hình dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét)
Phương pháp giải : Áp dụng Định lí hai tam giác đồng dạng để chứng minh $\Delta ABM\backsim \Delta CDM$. Từ đó suy ra tỉ số các cặp cạnh tương ứng để tính chiều cao của cây xanh. Lời giải chi tiết : Vì cột đèn và cây xanh đều vuông góc với mặt đất nên ta có \(\widehat A = \widehat C = {90^0}\) \( \Rightarrow \) AB // CD $\Rightarrow \Delta ABM\backsim \Delta CDM$ (Định lí hai tam giác đồng dạng) \(\begin{array}{l} \Rightarrow \frac{{AB}}{{AM}} = \frac{{CD}}{{CM}}\\\frac{{AB}}{{4,8}} = \frac{{10}}{{2 + 4,8}} = \frac{{10}}{{6,8}}\\ \Rightarrow AB = 4,8.\frac{{10}}{{6,8}} \approx 7\left( m \right)\end{array}\) Vậy chiều cao của cây xanh đó là khoảng 7m. Câu 4 : Cho tam giác ABC vuông tại A (AB > AC). Gọi I là trung điểm của AB. Kẻ IN vuông góc với BC tại N (N thuộc BC). a) Chứng minh $\Delta ACB\backsim \Delta NIB$. Từ đó suy ra \(BA.BI = BC.BN\). b) Giả sử AC = 6cm, BC = 10cm. Tính BN. c) Chứng minh \(\widehat {IAN} = \widehat {ICN}\). d) Chứng minh \(A{C^2} = N{C^2} - N{B^2}\). Phương pháp giải : a) Chứng minh $\Delta ACB\backsim \Delta NIB$ (g.g) suy ra tỉ số bằng nhau của các cặp cạnh tương ứng. b) Dựa vào định lí Pythagore để tính AB. Sử dụng tỉ số bằng nhau của phần a để tính BN. c) Chứng minh $\Delta ABN\backsim \Delta CBI$ (c.g.c) để chứng minh \(\widehat {IAN} = \widehat {ICN}\). d) Kẻ \(AH \bot BC\) tại H. Chứng minh \(A{C^2} = CH.CB\). Chứng minh BN = NH. Sử dụng hằng đẳng thức hiệu hai bình phương để chứng minh \(A{C^2} = CH.CB = N{C^2} - N{B^2}\). Chú ý: Độ dài các cạnh chỉ sử dụng cho ý b nên không được tính độ dài cạnh để chứng minh. Lời giải chi tiết :
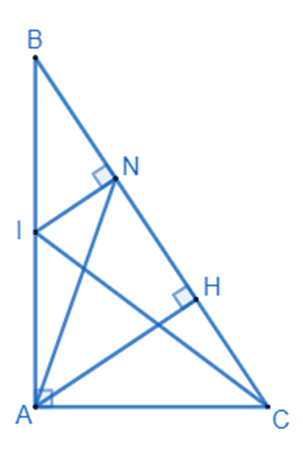
a) Xét \(\Delta ACB\) và \(\Delta NIB\) có: \(\widehat B\) chung \(\widehat A = \widehat N\left( { = {{90}^0}} \right)\) $\Rightarrow \Delta ACB\backsim \Delta NIB\left( g.g \right)$ (đpcm) \( \Rightarrow \frac{{BA}}{{BN}} = \frac{{BC}}{{BI}}\) \( \Rightarrow BA.BI = BC.BN\) (đpcm) b) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có: \(\begin{array}{l}A{B^2} = B{C^2} - A{C^2} = {10^2} - {6^2} = 64\\ \Rightarrow AB = 8\left( {cm} \right)\end{array}\) I là trung điểm của AB nên AI = IB = \(\frac{1}{2}\)AB = 4cm Ta có: \(BA.BI = BC.BN\) \(\begin{array}{l}8.4 = 10.BN\\ \Rightarrow BN = \frac{{8.4}}{{10}} = 3,2\left( {cm} \right)\end{array}\) c) Xét \(\Delta ABN\) và \(\Delta CBI\) có: \(\frac{{BA}}{{BN}} = \frac{{BC}}{{BI}}\left( {cmt} \right)\) \(\widehat B\) chung $\Rightarrow \Delta ABN\backsim \Delta CBI\left( c.g.c \right)$ \( \Rightarrow \widehat {IAN} = \widehat {ICN}\) (đpcm) d) Kẻ \(AH \bot BC\) tại H. Xét \(\Delta AHC\) và \(\Delta BAC\) có: \(\widehat A = \widehat H\left( { = {{90}^0}} \right)\) \(\widehat C\) chung $\Rightarrow \Delta AHC\backsim \Delta BAC\left( g.g \right)$ \( \Rightarrow \frac{{AC}}{{CH}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = CH.BC\). Vì \(IN \bot BC;AH \bot BC \Rightarrow IN//AH\) Xét tam giác ABH có IN // AH, I là trung điểm của AB nên IN là đường trung bình của tam giác ABH. \( \Rightarrow \) N là trung điểm của BH \( \Rightarrow BN = NH\). Ta có: \(CH.CB\)\( = \left( {CN - NH} \right)\left( {CN + BN} \right)\)\( = \left( {CN - BN} \right)\left( {CN + BN} \right)\)\( = C{N^2} - B{N^2}\) \( \Rightarrow A{C^2} = C{N^2} - B{N^2}\) (đpcm) Câu 5 : Chứng minh rằng nếu a, b, c khác nhau đôi một thì: \(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\). Phương pháp giải : Áp dụng đẳng thức \(\frac{1}{a} - \frac{1}{b} = \frac{{b - a}}{{ab}}\) Lời giải chi tiết : Xét phân thức \(\frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{{a - c - a + b}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{{a - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} - \frac{{a - b}}{{\left( {a - b} \right)\left( {a - c} \right)}}\)\( = \frac{1}{{a - b}} - \frac{1}{{a - c}}\). Tương tự ta có: \(\frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} = \frac{1}{{b - c}} - \frac{1}{{b - a}}\) \(\frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}} = \frac{1}{{c - a}} - \frac{1}{{c - b}}\) \( \Rightarrow \frac{{b - c}}{{\left( {a - b} \right)\left( {a - c} \right)}} + \frac{{c - a}}{{\left( {b - c} \right)\left( {b - a} \right)}} + \frac{{a - b}}{{\left( {c - a} \right)\left( {c - b} \right)}}\) \( = \frac{1}{{a - b}} - \frac{1}{{a - c}} + \frac{1}{{b - c}} - \frac{1}{{b - a}} + \frac{1}{{c - a}} - \frac{1}{{c - b}}\) \( = \frac{1}{{a - b}} + \frac{1}{{c - a}} + \frac{1}{{b - c}} + \frac{1}{{a - b}} + \frac{1}{{c - a}} + \frac{1}{{b - c}}\) \( = \frac{2}{{a - b}} + \frac{2}{{b - c}} + \frac{2}{{c - a}}\) (đpcm).
|
