Đề thi giữa kì 2 Toán 8 - Đề số 1 - Kết nối tri thứcĐã có lời giải SGK Toán lớp 9 - Kết nối tri thức (mới) Đầy đủ - Chi tiết - Chính xác Đề bài I. Trắc nghiệm Khoanh tròn trước câu trả lời đúng. Câu 1 : Biểu thức nào sau đây không phải là phân thức đại số?
Câu 2 : Với điều kiện nào của x thì phân thức \(\frac{{x + 2}}{{3 - x}}\) xác định
Câu 3 : Rút gọn phân thức \(\frac{{{x^2} - {y^2}}}{{{{\left( {x + y} \right)}^2}}}\) được kết quả bằng
Câu 4 : Thực hiện phép tính \(\frac{{x - 1}}{{x - y}} + \frac{{1 - y}}{{y - x}}\) ta được kết quả là
Câu 5 : Kết quả phép tính \(\frac{{5x + 2}}{{3x{y^2}}}:\frac{{10x + 4}}{{{x^2}y}}\) là
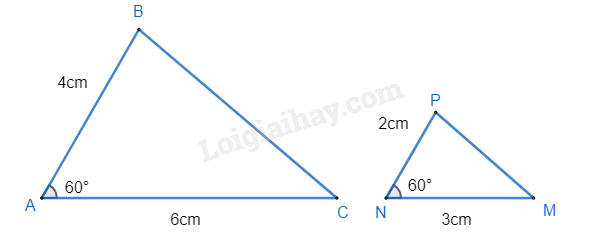
Câu 6 : Cho \(\Delta ABC\) có \(\widehat A = {60^0},AB = 4cm,AC = 6cm\); \(\Delta MNP\) có \(\widehat N = {60^0},MN = 3cm,NP = 2cm\). Cách viết nào sau đây đúng?
Câu 7 : Cho hình thang ABCD (AB // CD), hai đường chéo AC và BD cắt nhau tại I. Biết AB = 16cm, CD = 40 cm. Khi đó $\Delta AIB\backsim \Delta CID$ với tỉ số là:
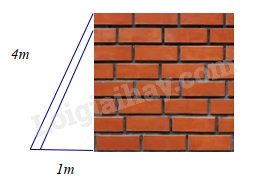
Câu 8 : Tính chiểu cao của bức tường hình bên biết chiều cao của thang là 4m và chân thang cách tường là 1m.
II. Tự luận Câu 1 : Cho biểu thức \(A = \left( {\frac{1}{{x - 2}} - \frac{{2x}}{{4 - {x^2}}} + \frac{1}{{2 + x}}} \right).\left( {\frac{2}{x} - 1} \right)\) a) Rút gọn A. b) Tính giá trị của biểu thức A tại x thỏa mãn: \({x^2} + 3x = 0\). c) Tìm x để \(A = \frac{1}{2}\). d) Tìm x nguyên để A nguyên dương. Câu 2 : Một tổ sản xuất phải làm 600 sản phẩm trong một thời gian quy định. Do tăng năng suất lao động, mỗi ngày tổ sản xuất đó làm được nhiều hơn kế hoạch 10 sản phẩm. Gọi x (sản phẩm) là số sản phẩm mà tổ sản xuất phải làm trong mỗi ngày theo kế hoạch (\(x \in \mathbb{N}*;x < 600\)). a) Viết biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc trước kế hoạch. b) Giả sử mỗi ngày họ dự định làm 40 sản phẩm. Hãy tính thời gian tổ hoàn thành công việc trước kế hoạch. Câu 3 : Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\)m, \(BC = 30\)m và \(B'C' = 40\)m. Tính độ rộng \(x\) của khúc sông.
Câu 4 : Cho \(\Delta ABC\) có AB = 18cm, AC = 24cm, BC = 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt AC, AB lần lượt tại D, E. a) Chứng minh rằng $\Delta ABC\backsim \Delta MDC$. b) Tính độ dài các cạnh của \(\Delta MDC\). c) Tính độ dài BE, EC. Lời giải và đáp án I. Trắc nghiệm Khoanh tròn trước câu trả lời đúng. Câu 1 : Biểu thức nào sau đây không phải là phân thức đại số?
Đáp án : D Phương pháp giải : Phân thức đại số là biểu thức có dạng \(\frac{A}{B}\), trong đó A, B là những đa thức và B khác đa thức 0. Lời giải chi tiết : Ta có: \(2{y^2} - 3 = \frac{{2{y^2} - 3}}{1}\), \(x + 1 = \frac{{x + 1}}{1}\) nên \(2{y^2} - 3,x + 1\) là phân thức đại số. A, B đúng. \(\frac{{5 - x}}{{x + 1}}\) (với \(x \ne - 1\)) là phân thức đại số vì \(5 - x,x + 1\) là đa thức và \(x \ne - 1 \Rightarrow x - 1 \ne 0\). C đúng. \(\frac{{x - 3}}{0}\) không phải phân thức đại số vì mẫu thức phải là một đa thức khác 0. D sai. Câu 2 : Với điều kiện nào của x thì phân thức \(\frac{{x + 2}}{{3 - x}}\) xác định
Đáp án : B Phương pháp giải : Để phân thức xác định thì mẫu thức khác 0. Lời giải chi tiết : Phân thức \(\frac{{x + 2}}{{3 - x}}\) xác định khi \(3 - x \ne 0\) hay \(x \ne 3\). Câu 3 : Rút gọn phân thức \(\frac{{{x^2} - {y^2}}}{{{{\left( {x + y} \right)}^2}}}\) được kết quả bằng
Đáp án : A Phương pháp giải : Thực hiện rút gọn phân thức theo 2 bước: + Bước 1: Phân tích tử và mẫu thành nhân tử (nếu cần). + Bước 2: Tìm nhân tử chung của tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó. Lời giải chi tiết : Ta có: \(\frac{{{x^2} - {y^2}}}{{{{\left( {x + y} \right)}^2}}} = \frac{{\left( {x - y} \right)\left( {x + y} \right)}}{{{{\left( {x + y} \right)}^2}}} = \frac{{x - y}}{{x + y}}\). Câu 4 : Thực hiện phép tính \(\frac{{x - 1}}{{x - y}} + \frac{{1 - y}}{{y - x}}\) ta được kết quả là
Đáp án : C Phương pháp giải : Đưa hai phân thức về cùng mẫu để cộng hai phân thức. Lời giải chi tiết : Ta có: \(\frac{{x - 1}}{{x - y}} + \frac{{1 - y}}{{y - x}}\) \( = \frac{{x - 1}}{{x - y}} + \frac{{y - 1}}{{x - y}}\) \( = \frac{{x - 1 + y - 1}}{{x - y}}\) \( = \frac{{x + y - 2}}{{x - y}}\). Câu 5 : Kết quả phép tính \(\frac{{5x + 2}}{{3x{y^2}}}:\frac{{10x + 4}}{{{x^2}y}}\) là
Đáp án : D Phương pháp giải : Sử dụng quy tắc chia hai phân thức. Lời giải chi tiết : Ta có: \(\frac{{5x + 2}}{{3x{y^2}}}:\frac{{10x + 4}}{{{x^2}y}}\)\( = \frac{{5x + 2}}{{3x{y^2}}}.\frac{{{x^2}y}}{{10x + 4}}\)\( = \frac{{\left( {5x + 2} \right).{x^2}y}}{{3x{y^2}.\left( {10x + 4} \right)}}\)\( = \frac{{\left( {5x + 2} \right){x^2}y}}{{3x{y^2}.2\left( {5x + 2} \right)}}\)\( = \frac{x}{{6y}}\). Câu 6 : Cho \(\Delta ABC\) có \(\widehat A = {60^0},AB = 4cm,AC = 6cm\); \(\Delta MNP\) có \(\widehat N = {60^0},MN = 3cm,NP = 2cm\). Cách viết nào sau đây đúng?
Đáp án : C Phương pháp giải : Dựa vào các trường hợp đồng dạng của hai tam giác. Lời giải chi tiết :
Xét tam giác ABC và tam giác NPM có: \(\widehat A = \widehat N\left( { = {{60}^0}} \right)\) \(\frac{{AB}}{{NP}} = \frac{{AC}}{{NM}}\left( {\frac{4}{2} = \frac{6}{3} = 2} \right)\) $\Rightarrow \Delta ABC\backsim \Delta NPM\left( c.g.c \right)$. Các góc tương ứng bằng nhau là: \(\widehat A = \widehat N;\widehat B = \widehat P;\widehat C = \widehat M\). \( \Rightarrow \) Cách viết đúng là: $\Delta BAC\backsim \Delta PNM$. Câu 7 : Cho hình thang ABCD (AB // CD), hai đường chéo AC và BD cắt nhau tại I. Biết AB = 16cm, CD = 40 cm. Khi đó $\Delta AIB\backsim \Delta CID$ với tỉ số là:
Đáp án : C Phương pháp giải : Chứng minh, tính tỉ số của cặp cạnh tương ứng trong hai tam giác. Lời giải chi tiết : Xét \(\Delta AIB\) và \(\Delta CID\) có: \(\widehat {BAI} = \widehat {ICD}\) (hai góc so le trong) \(\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh) $\Rightarrow \Delta AIB\backsim \Delta CID\left( g.g \right)$ \( \Rightarrow \) Tỉ số k của \(\Delta AIB\) và \(\Delta CID\) là: \(k = \frac{{AB}}{{CD}} = \frac{{16}}{{40}} = \frac{2}{5}\). Câu 8 : Tính chiểu cao của bức tường hình bên biết chiều cao của thang là 4m và chân thang cách tường là 1m.
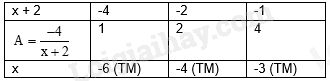
Đáp án : B Phương pháp giải : Áp dụng định lí Pythagore để tính chiều cao của thang. Lời giải chi tiết : Áp dụng định lí Pythagore trong tam giác vuông, ta có chiều cao của thang là: \(\sqrt {{4^2} - {1^2}} = \sqrt {15} \)(m) II. Tự luận Câu 1 : Cho biểu thức \(A = \left( {\frac{1}{{x - 2}} - \frac{{2x}}{{4 - {x^2}}} + \frac{1}{{2 + x}}} \right).\left( {\frac{2}{x} - 1} \right)\) a) Rút gọn A. b) Tính giá trị của biểu thức A tại x thỏa mãn: \({x^2} + 3x = 0\). c) Tìm x để \(A = \frac{1}{2}\). d) Tìm x nguyên để A nguyên dương. Phương pháp giải : a) Tìm điều kiện để các phân thức xác định. Sử dụng các quy tắc tính với phân thức đại số để rút gọn A. b) Tìm x thỏa mãn \({x^2} + 3x = 0\). Thay x vừa tìm được để tính giá trị của A. c) Thay \(A = \frac{1}{2}\) để tìm x. d) Để A nguyên dương thì tử thức phải chia hết cho mẫu thức, tử thức và mẫu thức phải cùng dấu. Lời giải chi tiết : a) ĐKXĐ: \(\left\{ \begin{array}{l}x - 2 \ne 0\\4 - {x^2} \ne 0\\2 + x \ne 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne - 2\\x \ne 0\end{array} \right.\) Ta có: \(A = \left( {\frac{1}{{x - 2}} - \frac{{2x}}{{4 - {x^2}}} + \frac{1}{{2 + x}}} \right).\left( {\frac{2}{x} - 1} \right)\) \(\begin{array}{l} = \left( {\frac{1}{{x - 2}} + \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{x + 2}}} \right).\left( {\frac{{2 - x}}{x}} \right)\\ = \left( {\frac{{x + 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{2x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{x - 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right).\left( {\frac{{2 - x}}{x}} \right)\\ = \frac{{x + 2 + 2x + x - 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\frac{{2 - x}}{x}\\ = \frac{{4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\frac{{2 - x}}{x}\\ = \frac{{ - 4}}{{x + 2}}\end{array}\) Vậy \(A = \frac{{ - 4}}{{x + 2}}\). b) Ta có: \({x^2} + 3x = 0\) \(\begin{array}{l}x\left( {x + 3} \right) = 0\\\left[ \begin{array}{l}x = 0\,\left( L \right)\\x = - 3\,\left( {TM} \right)\end{array} \right.\end{array}\) Thay \(x = - 3\) vào A, ta được: \(A = \frac{{ - 4}}{{ - 3 + 2}} = \frac{{ - 4}}{{ - 1}} = 4\) Vậy \(A = 4\) tại x thỏa mãn: \({x^2} + 3x = 0\). c) Để \(A = \frac{1}{2}\) thì \(\frac{{ - 4}}{{x + 2}} = \frac{1}{2}\) \(\begin{array}{l} \Rightarrow - 4.2 = x + 2\\x + 2 = - 8\\x = - 10\end{array}\) Vậy \(x = - 10\) thì \(A = \frac{1}{2}\). d) Đề A nguyên dương thì \(\frac{{ - 4}}{{x + 2}}\) nguyên dương \( \Rightarrow - 4 \vdots \left( {x + 2} \right)\) và \(x + 2 < 0\) hay \(\left( {x + 2} \right) \in \) Ước nguyên âm của -4. Mà Ước âm của -4 là: \(\left\{ { - 1; - 2; - 4} \right\}\) Ta có bảng giá trị sau:
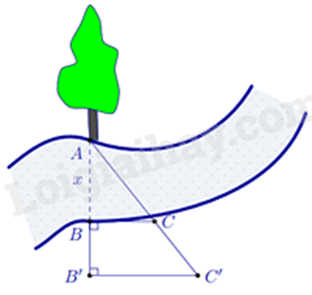
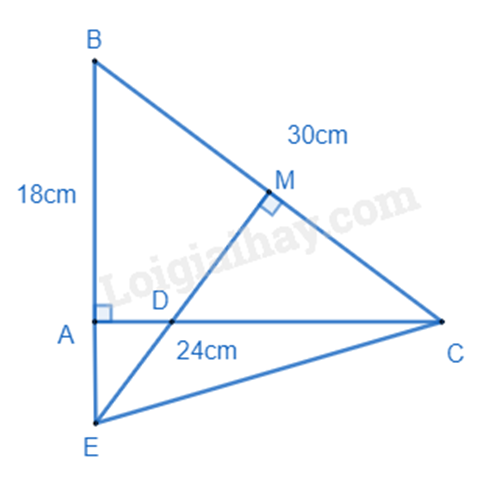
Vậy các giá trị của x để A nguyên dương là: \(x \in \left\{ { - 6; - 4; - 3} \right\}\). Câu 2 : Một tổ sản xuất phải làm 600 sản phẩm trong một thời gian quy định. Do tăng năng suất lao động, mỗi ngày tổ sản xuất đó làm được nhiều hơn kế hoạch 10 sản phẩm. Gọi x (sản phẩm) là số sản phẩm mà tổ sản xuất phải làm trong mỗi ngày theo kế hoạch (\(x \in \mathbb{N}*;x < 600\)). a) Viết biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc trước kế hoạch. b) Giả sử mỗi ngày họ dự định làm 40 sản phẩm. Hãy tính thời gian tổ hoàn thành công việc trước kế hoạch. Phương pháp giải : a) Viết biểu thức biểu thị thời gian hoàn thành theo kế hoạch, biểu thức biểu thị thời gian hoàn thành thực tế: Thời gian = tổng số sản phẩm : số sản phẩm làm được trong một ngày. Biểu thức biểu thị thời gian tổ hoàn thành công việc trước kế hoạch = thời gian theo kế hoạch – thời gian thực tế. b) Thay x = 40 vào biểu thức biểu thị thời gian tổ hoàn thành công việc trước kế hoạch. Lời giải chi tiết : a) Biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc theo kế hoạch là: \(\frac{{600}}{x}\) (ngày) Biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc thực tế là: \(\frac{{600}}{{x + 10}}\) (ngày) Vậy biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc trước kế hoạch là: \(\frac{{600}}{x} - \frac{{600}}{{x + 10}}\) (ngày) b) Vì mỗi ngày họ dự định làm 40 sản phẩm nên \(x = 40\) (sản phẩm). Thay \(x = 40\) vào biểu thức biểu thị theo x thời gian tổ hoàn thành công việc trước kế hoạch, ta được: \(\frac{{600}}{{40}} - \frac{{600}}{{40 + 10}} = 15 - 12 = 3\) (ngày). Vậy tổ hoàn thành công việc trước kế hoạch 3 ngày. Câu 3 : Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\)m, \(BC = 30\)m và \(B'C' = 40\)m. Tính độ rộng \(x\) của khúc sông.
Phương pháp giải : Áp dụng định lí của tam giác bằng nhau, chứng minh $\Delta ABC\backsim \Delta AB'C'$. Từ đó suy ra tỉ số bằng nhau giữa các cặp cạnh tương ứng. Lời giải chi tiết : Ta có: \(\widehat B = \widehat {B'} = {90^0} \Rightarrow \) BC // B’C’. Áp dụng định lí hai tam giác đồng dạng, ta có $\Delta ABC\backsim \Delta AB'C'$. \( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) \(\frac{x}{{x + 20}} = \frac{{30}}{{40}} = \frac{3}{4}\) \(\begin{array}{l} \Rightarrow 4x = 3\left( {x + 20} \right)\\4x = 3x + 60\\x = 60\left( m \right)\end{array}\) Vậy độ rộng x của khúc sông là 60m. Câu 4 : Cho \(\Delta ABC\) có AB = 18cm, AC = 24cm, BC = 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt AC, AB lần lượt tại D, E. a) Chứng minh rằng $\Delta ABC\backsim \Delta MDC$. b) Tính độ dài các cạnh của \(\Delta MDC\). c) Tính độ dài BE, EC. Phương pháp giải : a) Sử dụng định lí Pythagore đảo để chứng minh \(\Delta ABC\) vuông. Chứng minh $\Delta ABC\backsim \Delta MDC\left( g.g \right)$ b) Vì M là trung điểm của BC nên tính được MC. Từ phần a có $\Delta ABC\backsim \Delta MDC$ suy ra tỉ số của các cặp cạnh tương ứng trong hai tam giác để tính MD và CD. c) Chứng minh $\Delta BME\backsim \Delta BAC\left( g.g \right)$, tính được BE. Chứng minh \(\Delta BME = \Delta CME\left( {c.g.c} \right)\) suy ra CE. Lời giải chi tiết :
a) Xét \(\Delta ABC\) có: \(A{B^2} + A{C^2} = {18^2} + {24^2} = 900 = {30^2} = B{C^2}\) \( \Rightarrow \Delta ABC\) vuông tại A (định lí Pythagore đảo) Xét \(\Delta ABC\) và \(\Delta MDC\), ta có: \(\widehat A = \widehat M\left( { = {{90}^0}} \right)\) \(\widehat C\) chung $\Rightarrow \Delta ABC\backsim \Delta MDC\left( g.g \right)$ (đpcm) b) Ta có: M là trung điểm của BC nên \(BM = CM = \frac{1}{2}BC = \frac{1}{2}.30 = 15\left( {cm} \right)\) Vì $\Delta ABC\backsim \Delta MDC$ nên ta có: \(\frac{{AB}}{{MD}} = \frac{{BC}}{{CD}} = \frac{{AC}}{{MC}}\) \(\frac{{18}}{{MD}} = \frac{{30}}{{CD}} = \frac{{24}}{{15}} = \frac{8}{5}\) \( \Rightarrow MD = 18:\frac{8}{5} = 11,25\) \(CD = 30:\frac{8}{5} = 18,75\) c) Xét \(\Delta BME\) và \(\Delta BAC\) có: \(\widehat M = \widehat A\left( { = {{90}^o}} \right)\) \(\widehat B\) chung $\Rightarrow \Delta BME\backsim \Delta BAC\left( g.g \right)$ \( \Rightarrow \frac{{BE}}{{BC}} = \frac{{BM}}{{AB}}\) \(\frac{{BE}}{{30}} = \frac{{15}}{{18}} = \frac{5}{6} \Rightarrow BE = \frac{5}{6}.30 = 25\left( {cm} \right)\) Xét \(\Delta BME\) và \(\Delta CME\) có: BM = CM (M là trung điểm của BC) \(\widehat {BME} = \widehat {CME}\left( { = {{90}^0}} \right)\) ME chung \( \Rightarrow \Delta BME = \Delta CME\left( {c.g.c} \right)\) \( \Rightarrow BE = CE = 25cm\).
|
