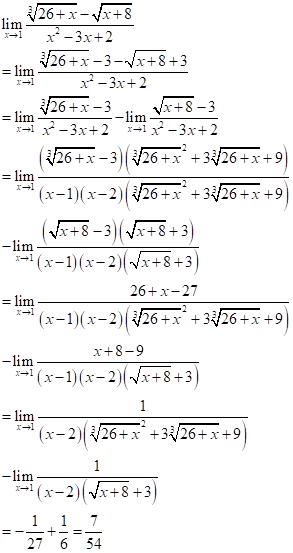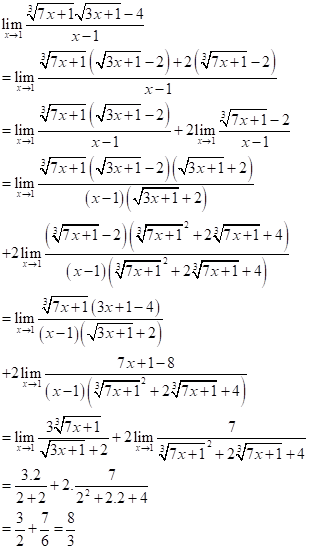Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 11

Đề bài

Câu 1: Phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại điểm có tung độ bằng 2 là:

A. \(y = - 2x + 10\)

B. \(y = - \frac{1}{2}x + \frac{1}{2}\)

C. \(y = - \frac{1}{2}x + \frac{7}{2}\)

D. \(y = - 2x + 7\)

Câu 2: Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc. Biết \(OA = OB = OC = a\), tính diện tích tam giác \(ABC\).

A. \(\frac{{{a^2}\sqrt 3 }}{4}\) B. \(\frac{{{a^2}\sqrt 3 }}{2}\)

C. \(\frac{{{a^2}\sqrt 2 }}{3}\) D. \(\frac{{{a^2}\sqrt 6 }}{2}\)

Câu 3: Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),\,\,\Delta ABC\) vuông tại \(B,\,\,AH\) là đường cao của \(\Delta SAB\), \(AK\) là đường cao của \(\Delta SAC\). Khẳng định nào sau đây sai?

A. \(AH \bot HK\)

B. \(AH \bot AC\)

C. \(AH \bot BC\)

D. \(AH \bot SC\)

Câu 4: Cho tứ diện \(S.ABC\) có \(G\) là trọng tâm tam giác \(ABC\), điểm \(M\) nằm trên đoạn \(SA\) sao cho \(AM = 2MS\). Mệnh đề nào dưới đây đúng?

A. \(\overrightarrow {MG} = - \frac{1}{6}\overrightarrow {SA} + \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} \)

B. \(\overrightarrow {MG} = \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} \)

C. \(\overrightarrow {MG} = - \frac{1}{3}\overrightarrow {SA} + \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} \)

D. \(\overrightarrow {MG} = \frac{2}{3}\overrightarrow {SA} + \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} \)

Câu 5: Biết giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x + 1} \right) = a\). Tính giá trị của \(2a + 1\).

A. \( - 1\) B. \( - 3\)

C. \(0\) D. \(3\)

Câu 6: Tính giới hạn \(\lim \frac{{{1^2} + {2^2} + {3^2} + ... + {n^2}}}{{{n^3} + 3n}}\).

A. \(\frac{1}{3}\) B. \(1\)

C. \(\frac{1}{4}\) D. \(2\)

Câu 7: Cho hàm số \(f\left( x \right)\) xác định bởi: \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 2}}{{x - 2}}\,\,khi\,\,x \ne 2\\2\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 2\end{array} \right.\). Tìm khẳng định sai trong các khẳng định sau đây?

A. \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 4\)

B. \(f\left( 2 \right) = 2\)

C. Hàm số \(f\left( x \right)\) liên tục tại \(x = 2\)

D. Hàm số \(f\left( x \right)\) gián đoạn tại \(x = 2\)

Câu 8: Cho hàm số \(y = m{x^3} - {x^2} - x + 3\). Với giá trị nào của \(m\) thì phương trình \(y' = 0\) có hai nghiệm trái dấu?

A. \(m > - \frac{1}{3}\) B. \(m < - \frac{1}{3}\)

C. \(m < 0\) D. \(m > 0\)

Câu 9: Cho hàm số \(f\left( x \right)\) xác định bởi: \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} - 1}}{{{x^2} - 1}}\,\,\,khi\,\,x > 1\\ax + 2\,\,\,khi\,\,x \le 1\end{array} \right.\). Xác định \(a\) để hàm số \(f\left( x \right)\) liên tục tại \(x = 1\).

A. \( - \frac{1}{2}\) B. \(1\)

C. \(2\) D. \(\frac{1}{2}\)

Câu 10: Đạo hàm cấp hai của hàm số \(y = - \sin 2x + 1\) là hàm số nào sau đây?

A. \(4\cos 2x\)

B. \( - 4\sin 2x\)

C. \( - 2\sin 2x\)

D. \(4\sin 2x\)

Câu 11: Một chuyển động thẳng xác định bởi phương trình chuyển động \(S\left( t \right) = {t^3} + 3{t^2} + 5t + 2\), trong đó \(t\) tính bằng giây và \(S\left( t \right)\) tính bằng mét. Gia tốc của chuyển động khi \(t = 2\) bằng bao nhiêu?

A. \(12m/{s^2}\)

B. \(17m/{s^2}\)

C. \(20m/{s^2}\)

D. \(18m/{s^2}\)

Câu 12: Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {x + 3x - 2{x^3}} \right)\).

A. \( - 2\) B. \( + \infty \)

C. \( - \infty \) D. \(1\)

Câu 13: Tính giới hạn \(\lim \frac{{ - 4{n^3} - 5{n^2}}}{{{n^2} + 3{n^3}}}\).

A. \( - 5\) B. \( - \frac{5}{3}\)

C. \( - 4\) D. \( - \frac{4}{3}\)

Câu 14: Tính đạo hàm của hàm số \(y = {x^3}\sin x\).

A. \(y' = 3{x^2}\cos x\)

B. \(y' = {x^2}\left( {3\sin x + x\cos x} \right)\)

C. \(y' = 3{x^2}\sin x - {x^3}\cos x\)

D. \(y' = 3{x^2}\sin x\)

Câu 15: Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{26 + x}} - \sqrt {x + 8} }}{{{x^2} - 3x + 2}}\).

A. \(\frac{5}{{54}}\) B. \(\frac{7}{{54}}\)

C. \(\frac{7}{{55}}\) D. \(\frac{4}{{27}}\)

Câu 16: Cho hình chóp đều, chọn mệnh đề sai trong các mệnh đề sau:

A. Chân đường cao của hình chóp đều kẻ từ đỉnh trùng với tâm của đa giá đáy đó.

B. Đáy của hình chóp là một đa giác đều.

C. Các mặt bên của hình chóp là những tam giác cân.

D. Tất cả những cạnh bên của hình chóp đều bằng nhau.

Câu 17: Trong không gian, ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) được gọi là đồng phẳng nếu và chỉ nếu:

A. Chúng có giá cùng nằm trong một mặt phẳng.

B. Một trong ba vectơ là vectơ không.

C. Chúng có giá song song hoặc trùng nhau.

D. Chúng có giá song song với một mặt phẳng nào đó.

Câu 18: Cho hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} - 5\). Giải phương trình \(y'' = - 1\), khi đó ta được kết quả là:

A. \(x = \pm \sqrt 3 \)

B. \(x = 1\)

C. \(x = \pm 1\)

D. Phương trình vô nghiệm

Câu 19: Xét trong không gian, trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

B. Một mặt phẳng \(\left( \alpha \right)\) và một đường thẳng \(a\) cùng vuông góc với đường thẳng \(b\) thì \(\left( \alpha \right)\) song song với \(a\)

C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Câu 20: Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{7x + 1}}\sqrt {3x + 1} - 4}}{{x - 1}}\).

A. \(\frac{7}{4}\) B. \(\frac{8}{3}\)

C. \(\frac{{267}}{{100}}\) D. \(2,66\)

PHẦN TỰ LUẬN

Câu 1: (1,0 điểm) Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {3x + 6} - 3}}{{1 - x}}\)

b) \(\mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} + x} } \right)\)

Câu 2: (1,0 điểm) Chứng minh rằng phương trình sau luôn có nghiệm với mọi \(m\):

\(\cos x + m\cos 2x = 0\)

Câu 3: (1,0 điểm) Viết phương trình tiếp tuyến với đồ thị hàm số \(y = {x^3} - 3x + 1\) biết tiếp tuyến đi qua điểm \(I\left( {1; - 1} \right)\).

Câu 4: (2,0 điểm) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AD = 2a\), hình chiếu vuông góc của đỉnh \(S\) lên mặt đáy là điểm \(H\) thuộc đoạn thẳng \(AB\) sao cho \(2HA = HB\). Biết \(SA = a\sqrt 2 ,\,\,SH = a\).

a) Chứng minh rằng: \(\left( {SAB} \right) \bot \left( {SBC} \right)\).

b) Tính góc giữa \(SD\) và \(\left( {ABCD} \right)\)

c) Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {SHD} \right)\).

Lời giải chi tiết

A. PHẦN TRẮC NGHIỆM

 

Câu 1 (TH):

Phương pháp:

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là:

\(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).

Cách giải:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).

Cho \(y = 2 \Rightarrow \frac{{x + 1}}{{x - 1}} = 2\)\( \Leftrightarrow x + 1 = 2x - 2 \Leftrightarrow x = 3\)

Ta có: \(y' = \frac{{ - 2}}{{{{\left( {x - 1} \right)}^2}}}\)\( \Rightarrow y'\left( 3 \right) = \frac{{ - 2}}{{{2^2}}} = - \frac{1}{2}\) .

Vậy phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại điểm có tung độ bằng 2 là:

\(y = - \frac{1}{2}\left( {x - 3} \right) + 2\)\( \Leftrightarrow y = - \frac{1}{2}x + \frac{7}{2}\) .

Chọn C.

Câu 2 (TH):

Phương pháp:

Công thức tính diện tích tam giác đều cạnh \(a:\,\,S = \frac{{{a^2}\sqrt 3 }}{4}\).

Cách giải:

Dễ thấy \(\Delta OAB = \Delta OAC = \Delta OBC\,\,\left( {c.g.c} \right)\)\( \Rightarrow AB = AC = BC\)

\( \Rightarrow \) Tam giác \(ABC\) đều cạnh \(AB = \sqrt {O{A^2} + O{B^2}} \)\( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)

\({S_{ABC}} = \frac{{{{\left( {a\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}\).

Chọn B.

Câu 3 (TH):

Phương pháp:

\(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\)\( \Rightarrow d \bot \Delta \,\,\forall \Delta \subset \left( P \right)\) .

Cách giải:

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.\\ \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\\\left\{ \begin{array}{l}AH \bot BC\\AH \bot SB\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\\ \Rightarrow \left\{ \begin{array}{l}AH \bot HK\\AH \bot BC\\AH \bot SC\end{array} \right.\end{array}\)

Do đó các đáp án A, C, D đúng.

Chọn B.

Câu 4 (TH):

Phương pháp:

Sử dụng công thức ba điểm: \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} \) và công thức trọng tâm của tam giác: \(\overrightarrow {MG} = \frac{1}{3}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\) với \(G\) là trọng tâm tam giác \(ABC\), \(M\) là điểm bất kì.

Cách giải:

\(\begin{array}{l}\overrightarrow {MG} = \overrightarrow {MS} + \overrightarrow {SG} \\ = - \frac{1}{3}\overrightarrow {SA} + \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right)\\ = - \frac{1}{3}\overrightarrow {SA} + \frac{1}{3}\overrightarrow {SA} + \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} \\ = \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} \end{array}\)

Chọn B.

Câu 5 (VD):

Phương pháp:

Sử dụng phương pháp nhân liên hợp.

Cách giải:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x + 1} \right) = a\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1 - {{\left( {x + 1} \right)}^2}}}{{\sqrt {{x^2} + 1} - x - 1}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 2x}}{{\sqrt {{x^2} + 1} - x - 1}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 2}}{{ - \sqrt {1 + \frac{1}{{{x^2}}}} - 1 - \frac{1}{x}}}\\ = \frac{{ - 2}}{{ - 2}} = 1 = a\\ \Rightarrow 2a + 1 = 2.1 + 1 = 3\end{array}\)

Chọn D.

Câu 6 (VD):

Phương pháp:

+) Chứng minh \({1^2} + {2^2} + {3^2} + ... + {n^2}\)\( = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6},\)\(\forall n \ge 1,n \in \mathbb{Z}\) bằng phương pháp quy nạp.

+) Tính giới hạn bằng cách chia cả tử và mẫu cho \(n\) với số mũ là số mũ cao nhất của tử và mẫu.

Cách giải:

Bằng phương pháp quy nạp toán học ta chứng minh \({1^2} + {2^2} + {3^2} + ... + {n^2}\)\( = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6},\)\(\forall n \ge 1,n \in \mathbb{Z}\).

Đẳng thức trên đúng với \(n = 1\) vì \(1 = \frac{{1.2.3}}{6}\).

Giả sử đẳng thức trên đúng đến \(n = k\)

\( \Rightarrow {1^2} + {2^2} + ... + {k^2}\) \( = \frac{{k\left( {k + 1} \right)\left( {2k + 1} \right)}}{6}\)

Ta cần chứng minh nó đúng đến \(n = k + 1\), tức là cần chứng minh

\({1^2} + {2^2} + ... + {\left( {k + 1} \right)^2}\)\( = \frac{{\left( {k + 1} \right)\left( {k + 2} \right)\left( {2k + 3} \right)}}{6}\) .

Ta có:

\(\begin{array}{l}VT\\ = {1^2} + {2^2} + ... + {\left( {k + 1} \right)^2}\\ = \frac{{k\left( {k + 1} \right)\left( {2k + 1} \right)}}{6} + {\left( {k + 1} \right)^2}\\ = \frac{{\left( {k + 1} \right)\left( {2{k^2} + k + 6k + 6} \right)}}{6}\\ = \frac{{\left( {k + 1} \right)\left( {2{k^2} + 7k + 6} \right)}}{6}\\ = \frac{{\left( {k + 1} \right)\left( {k + 2} \right)\left( {2k + 3} \right)}}{6}\\ = VP\end{array}\)

\( \Rightarrow \) Đẳng thức được chứng minh. Khi đó ta có:

\(\begin{array}{l}\lim \frac{{{1^2} + {2^2} + {3^2} + ... + {n^2}}}{{{n^3} + 3n}}\\ = \lim \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{{6\left( {{n^3} + 3n} \right)}}\\ = \lim \frac{{1.\left( {1 + \frac{1}{n}} \right)\left( {2 + \frac{1}{n}} \right)}}{{6\left( {1 + \frac{3}{{{n^2}}}} \right)}}\\ = \frac{{1.1.2}}{{6.1}} = \frac{1}{3}\end{array}\)

Chọn A.

Câu 7 (TH):

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).

Cách giải:

Ta có \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} - 2}}{{x - 2}} = + \infty \)

\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{{x^2} - 2}}{{x - 2}} = - \infty \)

Do đó không tồn tại giới hạn của hàm số khi x tiến đến 2.

Do đó hàm số \(f\left( x \right)\) gián đoạn tại \(x = 2\).

Chọn D.

Câu 8 (TH):

Phương pháp:

+) Tính \(y'\).

+) Điều kiện để phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có 2 nghiệm trái dấu là \(ac < 0\).

Cách giải:

Ta có: \(y' = 3m{x^2} - 2x - 1 = 0\).

Để phương trình \(y' = 0\) có hai nghiệm trái dấu thì \(ac < 0\)\( \Leftrightarrow - 3m < 0 \Leftrightarrow m > 0\) .

Chọn D.

Câu 9 (TH):

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) .

Cách giải:

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^3} - 1}}{{{x^2} - 1}}\\ = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} + x + 1}}{{x + 1}} = \frac{3}{2}\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {ax + 2} \right)\\ = a + 2\end{array}\)

Để để hàm số \(f\left( x \right)\) liên tục tại \(x = 1\) thì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\)\( \Leftrightarrow a + 2 = \frac{3}{2} \Leftrightarrow a = - \frac{1}{2}\).

Chọn A.

Câu 10 (TH):

Phương pháp:

Sử dụng các công thức \(\left( {\sin kx} \right)' = k\cos kx;\)\(\left( {\cos kx} \right)' = - k\sin kx\).

Cách giải:

\(y' = - 2\cos 2x\)\( \Rightarrow y'' = 4\sin 2x\).

Chọn D.

Câu 11 (TH):

Phương pháp:

\(a\left( t \right) = S''\left( t \right)\).

Cách giải:

Ta có:

\(\begin{array}{l}v\left( t \right) = S'\left( t \right) = 3{t^2} + 6t + 5\\a\left( t \right) = v'\left( t \right) = 6t + 6\end{array}\).

\( \Rightarrow a\left( 2 \right) = 6.2 + 6 = 18\,\,\left( {m/{s^2}} \right)\).

Chọn D.

Câu 12 (TH):

Phương pháp:

Đặt \({x^3}\) ra ngoài, xét dấu và kết luận.

Cách giải:

\(\mathop {\lim }\limits_{x \to - \infty } \left( {x + 3x - 2{x^3}} \right)\)\( = \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( {\frac{1}{{{x^2}}} + \frac{3}{{{x^2}}} - 2} \right)\)\( = + \infty \).

Chọn B.

Câu 13 (TH):

Phương pháp:

Chia cả tử và mẫu cho \({n^3}\).

Cách giải:

\(\lim \frac{{ - 4{n^3} - 5{n^2}}}{{{n^2} + 3{n^3}}}\)\( = \lim \frac{{ - 4 - \frac{5}{n}}}{{\frac{1}{n} + 3}} = - \frac{4}{3}\).

Chọn D.

Câu 14 (VD):

Phương pháp:

Sử dụng quy tắc tính đạo hàm \(\left( {uv} \right)' = u'v + uv'\) và các công thức tính đạo hàm cơ bản.

Cách giải:

\(y' = 3{x^2}\sin x + {x^3}\cos x\)\( = {x^2}\left( {3\sin x + x\cos x} \right)\) .

Chọn B.

Câu 15 (VD):

Phương pháp:

Sử dụng phương pháp nhân với biểu thức liên hợp để khử dạng \(\frac{0}{0}\).

Cách giải:

Chọn B.

Câu 16 (TH):

Phương pháp:

Hình chóp đều là chóp có tất cả các cạnh bên bằng nhau và đáy là đa giác đều.

Cách giải:

Mệnh đề: Tất cả những cạnh bên của hình chóp đều bằng nhau là mệnh đề sai vì chóp đều cạnh bên và cạnh đáy của chóp có thể không bằng nhau.

Chọn D.

Câu 17 (NB):

Phương pháp:

Sử dụng khái niệm đồng phẳng của vectơ.

Cách giải:

Trong không gian, ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) được gọi là đồng phẳng nếu và chỉ nếu chúng có giá song song với một mặt phẳng nào đó.

Chọn D.

Câu 18 (TH):

Phương pháp:

Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\).

Cách giải:

\(\begin{array}{l}y' = {x^3} - 4x \Rightarrow y'' = 3{x^2} - 4\\y'' = - 1 \Leftrightarrow 3{x^2} = 3 \Leftrightarrow x = \pm 1\end{array}\)

Chọn C.

Câu 19 (TH):

Phương pháp:

Suy luận từng đáp án và chọn đáp án đúng.

Cách giải:

Mệnh đề đúng là: Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Chọn C.

Câu 20 (VDC):

Phương pháp:

Sử dụng phương pháp nhân với biểu thức liên hợp để khử dạng \(\frac{0}{0}\).

Cách giải:

Chọn B.

II. PHẦN TỰ LUẬN

Câu 1 (TH):

Phương pháp:

Sử dụng phương pháp nhân với biểu thức liên hợp để khử dạng \(\frac{0}{0}\).

Cách giải:

a) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {3x + 6} - 3}}{{1 - x}}\)\( = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {\sqrt {3x + 6} - 3} \right)\left( {\sqrt {3x + 6} + 3} \right)}}{{\left( {1 - x} \right)\left( {\sqrt {3x + 6} + 3} \right)}}\)

\(\begin{array}{l} = \mathop {\lim }\limits_{x \to 1} \frac{{3x + 6 - 9}}{{\left( {1 - x} \right)\left( {\sqrt {3x + 6} + 3} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{ - 3}}{{\sqrt {3x + 6} + 3}} = - \frac{3}{{3 + 3}}\\ = - \frac{1}{2}\end{array}\)

b) \(\mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} + x} } \right)\)\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{\left( {x + \sqrt {{x^2} + x} } \right)\left( {x - \sqrt {{x^2} + x} } \right)}}{{x - \sqrt {{x^2} + x} }}\)

\(\begin{array}{l} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - {x^2} - x}}{{x - \sqrt {{x^2} + x} }}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{x}{{\sqrt {{x^2} + x} - x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{ - \sqrt {1 + \frac{1}{x}} - 1}}\\ = - \frac{1}{2}\end{array}\).

Câu 2 (VD):

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\) và có \(f\left( a \right).f\left( b \right) < 0 \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất 1 nghiệm thuộc \(\left( {a;b} \right)\).

Cách giải:

Xét hàm số \(f\left( x \right) = \cos x + m\cos 2x\) ta có:

\(\begin{array}{l}f\left( {\frac{\pi }{4}} \right) = \cos \frac{\pi }{4} + m\cos \frac{\pi }{2}\\ = \frac{{\sqrt 2 }}{2} + m.0 = \frac{{\sqrt 2 }}{2} > 0\\f\left( {\frac{{3\pi }}{4}} \right) = \cos \frac{{3\pi }}{4} + m\cos \frac{{3\pi }}{2}\\ = - \frac{{\sqrt 2 }}{2} + m.0 = - \frac{{\sqrt 2 }}{2} < 0\end{array}\)

Hàm số \(f\left( x \right) = \cos x + m\cos 2x\) liên tục trên \(\mathbb{R}\)\( \Rightarrow \) liên tục trên \(\left( {\frac{\pi }{4};\frac{{3\pi }}{4}} \right)\) và có \(f\left( {\frac{\pi }{4}} \right).f\left( {\frac{{3\pi }}{4}} \right) < 0\)

\( \Rightarrow \) Phương trình \(\cos x + m\cos 2x = 0\) có ít nhất 1 nghiệm \(x \in \left( {\frac{\pi }{4};\frac{{3\pi }}{4}} \right)\).

Vậy phương trình \(\cos x + m\cos 2x = 0\) luôn có nghiệm với mọi \(m\).

Câu 3 (VD):

Phương pháp:

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là:

\(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).

Cách giải:

Gọi tiếp điểm là \(M\left( {{x_0};x_0^3 - 3{x_0} + 1} \right)\).

Ta có \(y' = 3{x^2} - 3\).

Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = {x_0}\) là:

\(y = \left( {3x_0^2 - 3} \right)\left( {x - {x_0}} \right)\)\( + x_0^3 - 3{x_0} + 1\,\,\left( d \right)\) .

Ta có \(I\left( {1; - 1} \right) \in d\)

\( \Rightarrow - 1 = \left( {3x_0^2 - 3} \right)\left( {1 - {x_0}} \right)\) \( + x_0^3 - 3{x_0} + 1\) .

\(\begin{array}{l} \Leftrightarrow - 1 = 3x_0^2 - 3x_0^3 - 3 + 3{x_0}\\ + x_0^3 - 3{x_0} + 1\\ \Leftrightarrow 2x_0^3 - 3x_0^2 + 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} = - \frac{1}{2}\end{array} \right.\end{array}\)

Khi \({x_0} = 1 \Rightarrow \left( d \right):\,\,y = - 1\).

Khi \({x_0} = - \frac{1}{2}\)\( \Rightarrow \left( d \right):\,\, - \frac{9}{4}\left( {x + \frac{1}{2}} \right) + \frac{{19}}{8}\) \( = - \frac{9}{4}x + \frac{5}{4}\) .

Câu 4 (VD):

Cách giải:

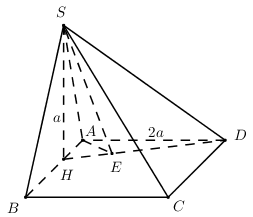
a) Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {SAB} \right)\) .

Mà \(BC \subset \left( {SBC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\).

b) \(SH \bot \left( {ABCD} \right) \Rightarrow HD\) là hình chiếu của \(SD\) trên \(\left( {ABCD} \right)\).

\( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right)\)\( = \angle \left( {SD;HD} \right) = \angle SDH\)

Trong tam giác vuông \(SAH:\)\(AH = \sqrt {S{A^2} - S{H^2}} = a\) .

Trong tam giác vuông \(ADH:\)\(HD = \sqrt {A{D^2} + A{H^2}} = a\sqrt 5 \).

Trong tam giác vuông \(SHD:\)\(\tan \angle SDH = \frac{{SH}}{{HD}}\) \( = \frac{a}{{a\sqrt 5 }} = \frac{1}{{\sqrt 5 }}\) .

\( \Rightarrow \angle SDH \approx {24^0}6'\)\( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) \approx {24^0}6'\).

c) Trong \(\left( {ABCD} \right)\) kẻ \(AE \bot HD\,\,\left( {E \in HD} \right)\) ta có :

\(\left\{ \begin{array}{l}AE \bot HD\\AE \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\)

\( \Rightarrow AE \bot \left( {SHD} \right)\) \( \Rightarrow d\left( {A;\left( {SHD} \right)} \right) = AE\)

Áp dụng hệ thức lượng trong tam giác vuông \(AHD\) ta có: \(AE = \frac{{AH.AD}}{{HD}}\)\( = \frac{{a.2a}}{{a\sqrt 5 }} = \frac{{2\sqrt 5 a}}{5}\)

Vậy \(d\left( {A;\left( {SHD} \right)} \right) = \frac{{2\sqrt 5 a}}{5}\).

xemloigiai.com