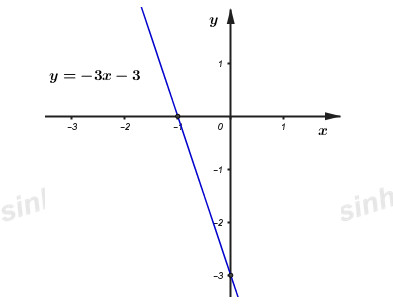
Đề số 1 - Đề kiểm tra học kì 1 - Toán 9Tải vềĐáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9 Lựa chọn câu để xem lời giải nhanh hơn Tải về Đề bài Bài 1: (2 điểm) 1) Thực hiện phép tính: a) √8−2√18+5√32−√(√2−1)2 b) 5+6√5√5+7−√7√7−1−(√5+√7) 2) Giải phương trình: x−√x−15=17. Bài 2: (2,5 điểm) Cho biểu thức P=3x+√9x−3x+√x−2−√x+1√x+2+√x−21−√x với x≥0,x≠1 a) Rút gọn biểu thức P. b) So sánh P với √P với điều kiện √Pcó nghĩa c) Tìm x để 1P nguyên. Câu 3: (2 điểm) Cho đường thẳng (d1):y=(m−1)x+2m+1. Tìm m để đường thẳng d1 cắt trục tung tại điểm có tung độ là −3. Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng (d):y=x+1 nằm trên trục hoành. Bài 4: (3 điểm) Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của (O) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N. a) Chứng minh DC=DN. b) Chứng minh AC là tiếp tuyến của đường tròn tâm O. c) Gọi H là chân đường vuông góc kẻ từ M xuống AB, I là trung điểm MH. Chứng minh B, C, I thẳng hàng. d) Qua O kẻ đường vuông góc với AB, cắt (O) tại K (K và M nằm khác phía với đường thẳng AB ). Tìm vị trí của M để diện tích tam giác MHK lớn nhất. Bài 5: (0,5 điểm) Cho các số thực dương x,y,z thỏa mãn x+2y+3z≥20. Tìm giá trị nhỏ nhất của biểu thức : A=x+y+z+3x+92y+4z. LG bài 1 Lời giải chi tiết: Bài 1: 1) Thực hiện phép tính: a)√8−2√18+5√32−√(√2−1)2=√22.2−2√32.2+5√42.2−|√2−1|=2√2−2.3√2+5.4√2−(√2−1)=2√2−6√2+20√2−√2+1=15√2+1. Vậy √8−2√18+5√32−√(√2−1)2=15√2+1 b)5+6√5√5+7−√7√7−1−(√5+√7)=√5.√5+6√5√5+√7.√7−√7√7−1−(√5+√7)=√5(6+√5)√5+√7.(√7−1)√7−1−√5−√7=6+√5+√7−√5−√7=6. Vậy 5+6√5√5+7−√7√7−1−(√5+√7)=6 2) Giải phương trình: x−√x−15=17. ĐKXĐ: x≥15 x−√x−15=17⇔x−17=√x−15⇔{x−17≥0(x−17)2=(√x−15)2⇔{x≥17x2−34x+289=x−15⇔{x≥17x2−35x+304=0 Xét phương trình x2−35x+304=0, ta có: x2−35x+304=0x2−16x−19x+304=0x(x−16)−19(x−16)=0(x−19)(x−16)=0⇔[x=19(TM)x=16(L) Vậy phương trình đã cho có nghiệm duy nhất là x=19. LG bài 2 Lời giải chi tiết: Cho biểu thức P=3x+√9x−3x+√x−2−√x+1√x+2+√x−21−√x với x≥0,x≠1 a) Rút gọn biểu thức P. ĐKXĐ: x≥0,x≠1 P=3x+√9x−3x+√x−2−√x+1√x+2+√x−21−√x=3x+√9x−3(x−√x)+(2√x−2)−√x+1√x+2+√x−21−√x=3x+3√x−3(√x+2).(√x−1)−(√x−1).(√x+1)(√x−1).(√x+2)+(√x−2)(√x+2)−(√x−1)(√x+2)=3x+3√x−3−(x−1)−(x−4)(√x−1)(√x+2)=x+3√x+2(√x−1)(√x+2)=(x+2√x)+(√x+2)(√x−1)(√x+2)=(√x+1)(√x+2)(√x−1)(√x+2)=√x+1√x−1. VậyP=√x+1√x−1. b) So sánh P với √P với điều kiện √Pcó nghĩa √P có nghĩa ⇔√x+1√x−1≥0⇔√x−1>0(do√x+1>0∀x≥0,x≠1) ⇔√x>1⇔x>1. Xét hiệu: P−√P=√x+1√x−1−√√x+1√x−1. ⇒P−√P=√x+1√x−1−√√x+1√x−1=√x+1√x−1−√√x+1√√x−1=√x+1√x−1−√(√x+1)(√x−1)(√√x−1)2=√x+1−√x−1√x−1. Ta có: √x−√x−1=(√x+√x−1)(√x−√x−1)√x+√x−1=x−(x−1)√x+√x−1=1√x+√x+1>0 Mà có: √x−1>0 (cmt) ⇒P−√P>0⇒P>√P với mọi x>1. c) Tìm x để 1P nguyên. Xét: 1P=√x−1√x+1=√x+1−2√x+1=1−2√x+1. Để 1P nguyên thì 2√x+1 nguyên, suy ra √x+1 là ước của 2. Mà √x+1>0 ⇒(√x+1)∈U(2)⇒(√x+1)={1;2}.⇒[√x+1=2√x+1=1⇔[√x=1√x=0⇔[x=1(ktm)x=0(tm). Vậy với x=0 thì 1P nguyên. LG bài 3 Lời giải chi tiết: Cho đường thẳng (d1):y=(m−1)x+2m+1. Tìm m để đường thẳng d1 cắt trục tung tại điểm có tung độ là −3. Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng (d):y=x+1 nằm trên trục hoành. Vì d1 cắt trục tung tại điểm có tung độ là −3, suy ra (0;−3) nằm trên đường thẳng d1 ⇒−3=(m−1).0+2m+1⇔2m=−4⇔m=−2. Với m=−2 ta có phương trình đường thẳng (d1):y=−3x−3. Nhận thấy: A(0;−3),B(−1;0) nằm trên đồ thị hàm số. Vì hàm số (d1):y=−3x−3 là hàm số bậc nhất nên đồ thị của nó có dạng đường thẳng, từ đó ta có đồ thị: Hoành độ giao điểm của (d1):y=−3x−3 và (d):y=x+1 là nghiệm của phương trình: x+1=−3x−3⇔4x=−4 ⇔x=−1⇒y=x+1=−1+1=0. Vậy giao điểm của (d1):y=−3x−3 và (d):y=x+1 là (−1;0). Nhận thấy điểm (−1;0) nằm trên trục hoành (do có tung độ bằng 0). Vậy ta có điều cần chứng minh. LG bài 4 Lời giải chi tiết:
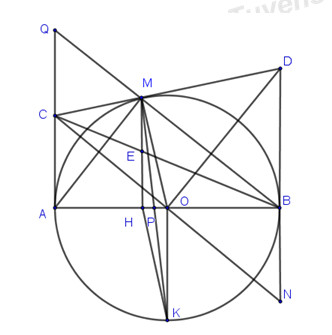
Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của (O) cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N. a) Chứng minh DC=DN. Xét đường tròn (O) có MD và BD là tiếp tuyến với B, D là tiếp điểm ⇒MD=DB(tính chất tiếp tuyến) Xét tam giác MOD và tam giác BOD có: MD=BD (cmt) MO=OB (cùng là bán kính đường tròn) OD chung ⇒ΔMOD=ΔBOD⇒∠MDO=∠BDO⇒OD là phân giác ∠MDB. Xét tam giác CDN có: OD là đường cao (doOD⊥CN) OD là phân giác ∠MDB Suy ra tam giác CDN cân tại D, suy ra CD=ND (đpcm) b) Chứng minh AC là tiếp tuyến của đường tròn tâm O. Xét tam giác CND cân tại D có OD là đường cao ứng với đỉnh D, suy ra OD đồng thời là trung trực ứng với cạnh CN, suy ra CO=ON Xét tam giác COA và tam giác BON có: CO=ON (cmt) OA=OB (do cùng là bán kính) ∠COA=∠BON (hai góc đối đỉnh) ⇒ΔCOA=ΔBON⇒∠CAO=∠NBO=90o Xét đường tròn tâm O có AC vuông góc với AO, AO là bán kính đường tròn, suy ra AC là tiếp tuyến của đường tròn (đpcm). c) Gọi H là chân đường vuông góc kẻ từ M xuống AB, I là trung điểm MH. Chứng minh B, C, I thẳng hàng. Kéo dài BM cắt AC tại Q, BC cắt MH tại E Xét tam giác BMD có DM=DB(cmt)⇒∠DMB=∠DBM Ta có: AB⊥AQ,AB⊥DN⇒AQ//DN. Mà có ∠CQM=∠MBD (so le trong) Lại có: ∠QMC=∠DMB (đối đỉnh) ⇒∠CQM=∠QMC, suy ra tam giác MCQ cân tại C, suy ra QC=MC Chứng minh tương tự như ở câu a ta có AC=MC (do tính chất tiếp tuyến) Suy ra QC=AC⇒QC=12QA. Xét tam giác BQC có ME song song với QC (cùng vuông góc với AB) ⇒MEQC=BMBQ (định lí Ta-lét) Chứng minh tương tự có MHAQ=BMBQ Suy ra MEQC=MHAQ. Mà có QC=12QA suy ra ME=12MH, suy ra E là trung điểm của MH. Mà theo đề bài có I là trung điểm của MH, suy ra I trùng với E, suy ra B, C, I thẳng hàng (đpcm). d) Qua O kẻ đường vuông góc với AB, cắt (O) tại K (K và M nằm khác phía với đường thẳng AB). Tìm vị trí của M để diện tích tam giác MHK lớn nhất. Gọi P là giao điểm của MK và AB. Không mất tính tổng quát, ta chọn bán kính đường tròn bằng 1, giả sử độ dài đoạn OH=a(0<a<1). ⇒MH=√OM2−OH2=√1−a2. Có MH song song với OK (do cùng vuông góc với AB) ⇒PHPO=MHOK=√1−a21⇒PH=√1−a2.OP. Ta có hệ: {PHPO=√1−a2PH+PO=OH=a⇒{PO=PH√1−a2PH+PH√1−a2=a⇒PH=a.√1−a2√1−a2+1⇒OP=a√1−a2+1. Ta có: SMHK=SMHP+SPKH=12MH.HP+12OK.HP=12(√1−a2.a√1−a2√1−a2+1+1.a√1−a2√1−a2+1)=12a√1−a2.√1−a2+1√1−a2+1=12a√1−a2. Áp dụng bất đẳng thức Cosi ta có: a√1−a2≤a2+1−a22=12 Dấu “=” xảy ra ⇔a=√1−a2⇒a=1√2 ⇒cos∠MOH=OHR=1√2⇒∠MOH=45o. Vậy M là điểm nằm trên đường tròn sao cho ∠MOH=45o là điểm thỏa mãn yêu cầu bài toán. LG bài 5 Lời giải chi tiết: Cho các số thực dương x,y,z thỏa mãn x+2y+3z≥20. Tìm giá trị nhỏ nhất của biểu thức : A=x+y+z+3x+92y+4z. Ta có: A=x+y+z+3x+92y+4z=14x+(34x+3x)+12y+(12y+92y)+34z+(14z+4z) Áp dụng bất đẳng thức Cosi cho các số dương ta có: +)34x+3x≥2√34x.3x=3+)12y+92y≥2√12y.92y=3+)14z+4z≥2√14z.4z=2 ⇒A≥14(x+2y+3z)+3+3+2=204+3+3+2=13. Dấu “=” xảy ra ⇔{34x=3x12y=92y14z=4z⇔{x=2y=3z=4.
|