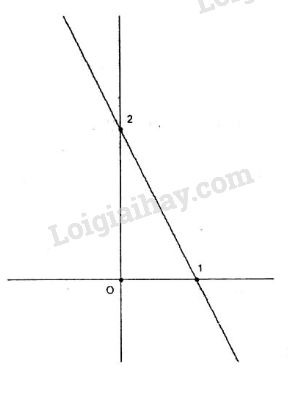
Đề kiểm tra 45 phút (1 tiết) - Chương 2, 3 - Đề số 2 - Đại số 10

Đề bài

Câu 1. Cho hàm số $y = 2mx + 1 - m{\rm{ }}(1)$ .

a.Lập bảng biến thiên và vẽ đồ thị hàm số (1) khi $m= -1.$

b.Tìm điểm cố định mà đồ thị hàm số (1) luôn đi qua khi m thay đổi.

c.Tìm m để đồ thị hàm số (1) cắt parabol $y = {x^2} + 2x - 2$ tại hai điểm phân biệt.

Câu 2.

a.Giải phương trình $\left( {{x^2} + x - 2} \right)\left( {{x^2} + x - 3} \right) = 12$ .

b.Giải và biện luận phương trình $\dfrac{{x - m}}{{x - 1}} = {m^2}$ theo tham số m.

Câu 3. Cho phương trình $m{x^2} - 2\left( {m + 1} \right)x + m + 2 = 0$ .

a. Xác định m để phương trình có một nghiệm bằng 2. Tìm nghiệm còn lại.

b. Xác định các giá trị nguyên của m để phương trình có hai nghiệm phân biệt sao cho tổng các nghiệm là một số nguyên.

Lời giải chi tiết

Câu 1.

a. Khi $m= -1$ ta có hàm số $y = - 2x + 2$ .

Tập xác định D=R.

Do a=-2 < 0 nên hàm số nghịch biến trên R.

$x = 0 \Rightarrow y = 2$ : Đồ thị cắt trục tung tại điểm (0;2).

$y = 0 \Rightarrow x = 1$ : Đồ thị cắt trục hoành tại điểm (1;0).

Đồ thị

b. Giả sử $\left( {{x_0};{y_0}} \right)$ là điểm đồ thị luôn luôn đi qua khi m thay đổi.

Ta có:

$\begin{array}{l} {y_0} = 2m{x_0} + 1 - m\\ \Leftrightarrow 2m{x_0} - m + 1 - {y_0} = 0\\ \Leftrightarrow \left( {2{x_0} - 1} \right)m + \left( {1 - {y_0}} \right) = 0 \end{array}$

Điểm M là điểm cố định mà đồ thị hàm số luôn đi qua

$\Leftrightarrow$ phương trình trên nghiệm đúng với mọi m

$\Leftrightarrow \left\{ \matrix{ 2{x_0} - 1 = 0 \hfill \cr 1 - {y_0} = 0 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ {x_0} = {1 \over 2} \hfill \cr {y_0} = 1 \hfill \cr} \right.$

Vậy đồ thị luôn luôn đi qua điểm $\left( {\dfrac{1}{2};1} \right)$ khi m thay đổi.

c. Phương trình hoành độ giao điểm parabol và đường thẳng

${x^2} + 2x - 2 = 2mx + 1 - m$

$\Leftrightarrow {x^2} + 2\left( {1 - m} \right)x + m - 3 = 0(*)$

Đường thẳng cắt Parabol tại hai điểm phân biệt $\Leftrightarrow (*)$ có hai nghiệm phân biệt.

Ta có:

$\Delta ' = {\left( {1 - m} \right)^2} - \left( {m - 3} \right)$$\, = {m^2} - 3m + 4$$\,= {\left( {m - \dfrac{3}{2}} \right)^2} + \dfrac{7}{4} > 0,\,\forall m \in \mathbb{R}$

Suy ra đường thẳng luôn luôn cắt parabol tại hai điểm phân biệt với mọi m.

Câu 2.

a. Xét phương trình $\left( {{x^2} + x - 2} \right)\left( {{x^2} + x - 3} \right) = 12$

Đặt $t = {x^2} + x - 2$ .Phương trình trở thành

$t\left( {t - 1} \right) = 12 \Leftrightarrow {t^2} - t - 12 = 0$

$\Leftrightarrow \left[ \matrix{ t = 4 \hfill \cr t = - 3 \hfill \cr} \right.$

Với: ${x^2} + x - 2 = 4 \Leftrightarrow {x^2} + x - 6 = 0$

$\Leftrightarrow \left[ \matrix{ x = - 3 \hfill \cr x = 2 \hfill \cr} \right.$

Với: ${x^2} + x - 2 = - 3 \Leftrightarrow {x^2} + x + 1 = 0$ . Phương trình vô nghiệm.

Kết luận: Phương trình đã cho có hai nghiệm $x= -3, x= 2.$

b. Xét phương trình $\dfrac{{x - m}}{{x - 1}} = {m^2}$ (1)

Điều kiện xác định: $x \ne 1$ .

Với điều kiện trên phương trình tương đương

$x - m = {m^2}\left( {x - 1} \right)$

$\begin{array}{l} \Leftrightarrow x - m = {m^2}x - {m^2}\\ \Leftrightarrow {m^2}x - x = {m^2} - m \end{array}$

$\Leftrightarrow \left( {{m^2} - 1} \right)x = {m^2} - m$ (2)

Với ${m^2} - 1 \ne 0 \Leftrightarrow m \ne \pm 1$ : Phương trình (2) có nghiệm duy nhất

$x = \dfrac{{{m^2} - m}}{{{m^2} - 1}} = \frac{{m\left( {m - 1} \right)}}{{\left( {m - 1} \right)\left( {m + 1} \right)}}= \dfrac{m}{{m - 1}}$

Nghiệm này thỏa mãn điều kiện $x \ne 1$ .

Với: ${m^2} - 1 = 0 \Leftrightarrow m = \pm 1$

+) $m= 1$ phương trình (2) trở thành $0x= 0$. Phương trình nghiệm đúng với mọi $x\in R$.

Suy ra phương trình (1) nghiệm đúng với mọi $x \ne 1$ .

+) $m= -1$ phương trình (2) trở thành $0x= 2$. Phương trình vô nghiệm.

Suy ra phương trình (1) vô nghiệm.

Kết luận:

$m \ne \pm 1:x = \dfrac{m}{{m - 1}}$

$m = 1:x \ne 1$

$m = - 1$ : Vô nghiệm

Câu 3.

a. Xét phương trình $m{x^2} - 2\left( {m + 1} \right)x + m + 2 = 0$.

Phương trình có nghiệm x= 2 khi: $4m - 4\left( {m + 1} \right) + m + 2 = 0$

$\begin{array}{l} \Leftrightarrow 4m - 4m - 4 + m + 2 = 0\\ \Leftrightarrow m - 2 = 0 \end{array}$

$\Leftrightarrow m = 2$ .

Khi đó phương trình trở thành $2{x^2} - 6x + 4 = 0$

$\Leftrightarrow \left[ \matrix{ x = 2 \hfill \cr x = 1 \hfill \cr} \right.$

Vậy phương trình có nghiệm $x= 2$ khi $m= 2$. Nghiệm còn lại là $x= 1$.

b. Ta có:

$\Delta ' = {\left( {m + 1} \right)^2} - m\left( {m + 2} \right) = 1 > 0$ .

Suy ra phương trình luôn có hai nghiệm phân biệt với $\forall m \ne 0$ .

Khi đó tổng các nghiệm là: $S = \dfrac{{2\left( {m + 1} \right)}}{m} = \dfrac{{2m + 2}}{m}= 2 + \dfrac{2}{m}$.

S là số nguyên khi và chỉ khi m là ước số của 2.

Vậy $m = \pm 1,m = \pm 2$ .

 xemloigiai.com