Đề kiểm tra 15 phút - Đề số 3 - Chương 3 - Hình học 11

Đề bài

Câu 1. Cho hai vec tơ \(\overrightarrow a \,,\,\,\overrightarrow b \) không cùng phương và vec tơ \(\overrightarrow c \). Điều kiện cần và đủ để ba vec tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \) đồng phẳng là:
A. Có cặp số m, n duy nhất sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b. \)

B. Có cặp số m, n sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \).

C. Có số m duy nhất sao cho \(\overrightarrow a + \overrightarrow b = m\overrightarrow c \).

D. Có số m sao cho \(\overrightarrow a + \overrightarrow b = m\overrightarrow c \).

Câu 2. Cho hình hộp ABCD.A’B’C’D’ . Tìm mệnh đề đúng.

A. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD} \).

B. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AB'} \).

C. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).

D. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD'} \).

Câu 3. Cho hình lập phương ABCD.EFGH, thực hiện phép toán \(\overrightarrow x = \overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CG} \).

A. \(\overrightarrow x = \overrightarrow {GE} \). B. \(\overrightarrow x = \overrightarrow {CE} \).

C. \(\overrightarrow x = \overrightarrow {CH} \). D. \(\overrightarrow x = \overrightarrow {EC} \).

Câu 4. Trong các mệnh đê sau đây, tìm mệnh đề đúng.

A. Nếu mp \(\left( \alpha \right)\) song song với mp \(\left( \beta \right)\) và đường thẳng \(a \subset \left( \alpha \right)\) thì a song song \(\left( \beta \right)\).

B. Nếu mp \(\left( \alpha \right)\) song song với mp \(\left( \beta \right)\) và đường thẳng \(a \subset \left( \alpha \right)\), đường thẳng \(b \subset \left( \beta \right)\) thì a song song với b.

C. Nếu đường thẳng a song song với mp \(\left( \alpha \right)\) và đường thẳng b song song \(\left( \beta \right)\) thì a song song song với b.

D. Nếu đường thẳng a song song với đường thẳng b và \(a \subset \left( \alpha \right)\,,\,\,b \subset \left( \beta \right)\) thì \(\left( \alpha \right)\,,\,\left( \beta \right)\) song song với nhau.

Câu 5. Cho hình chóp S.ABCD , với O là giao điểm của AC và BD. Mệnh đề nào sau đây đúng?

A. Nếu ABCD là hình bình hành thì \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).

B. Nếu \(SA + SC = SB + SD\) thì ABCD là hình bình hành.

C. Nếu ABCD là hình bình hành thì \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).

D. Nếu \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) thì ABCD là hình bình hành.

Câu 6. Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a. Tang của góc giữa AC và mặt phẳng (ABD) bằng:

A.\(\sqrt 5 \)

B. 1

C. Không xác định.

D. \(\dfrac{{\sqrt {51} }}{{17}}\).

Câu 7. Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.

B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.

D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

Câu 8. Chọn câu sai.

A. Qua một điểm O cho trước có duy nhất một mặt phẳng (P) vuông góc với đường thẳng a.

B. Nếu một đường thẳng vuông góc với hai cạnh cắt nhau của một ngũ giác trong mặt phẳng thì đường thẳng đó vuông góc với ba cạnh còn lại.

C. Nếu một đường thẳng vuông góc với hai cạnh của một tứ giác trong một mặt phẳng thì nó cũng vuông góc với hai cạnh còn lại

D. Trong một tam giác ABC, một đường thẳng vuông góc với hai cạnh của một tam giác thì nó vuông góc với cạnh còn lại.

Câu 9. Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp nào sau đây ?

A. \(GM = GN\).

B. \(\overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \).

C. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).

\(D.\overrightarrow {PG} = \dfrac{1}{4}\left( {\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} } \right)\) với P là điểm bất kì.

Câu 10. Cho hình chóp S.ABCD có đáy là hình thoi BACD cạnh A có góc \(\widehat {BAD} = {60^0}\) và SA = SB = SD =\(\frac{{a\sqrt 3 }}{2}\). Xác định số đo góc giữa hai mặt phẳng (SAC) và (ABCD) là:

A.30⁰ B. 60⁰

C. 45⁰ D. 90⁰

Lời giải chi tiết

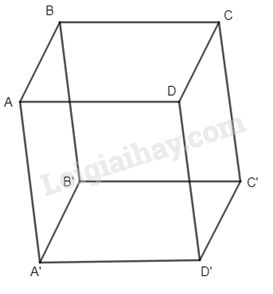
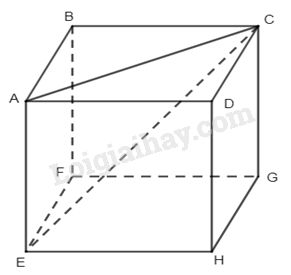
Câu 2.

Ta có \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \).

Chọn đáp án C.

Câu 3.

Ta có \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CG} = \overrightarrow {CA} + \overrightarrow {CG} = \overrightarrow {CE} \) . Chọn đáp án B.

Câu 5.

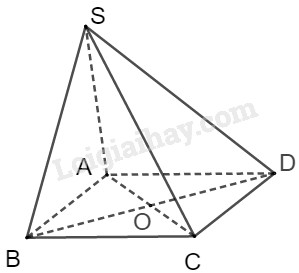
Đáp án A, B, C sai do thiếu dữ kiện nên chưa thể xác định. Đáp án D đúng do nếu \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) thì O là trung điểm chung của đoạn thẳng nối trung điểm AC và trung điểm BD mà O là giao hai đường chéo nên ABCD là hình bình hành.

Câu 6.

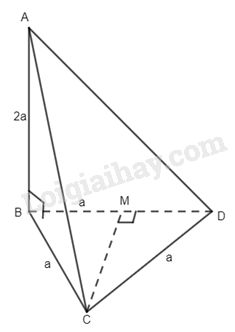
Lấy M là chân đường cao từ C kẻ xuống BD. Ta có

\(\left\{ \begin{array}{l}CM \bot BD\\CM \bot AB(\,AB \bot (BCD))\end{array} \right.\,\, \Rightarrow CM \bot \left( {ABD} \right)\)

Suy ra hình chiếu vuông góc của C xuống (ABD) là M.

\(\left( {AC,(ABD)} \right) = \left( {AC,AM} \right) = \widehat {MAC}\)

Xét tam giác AMC vuông tại M ( do có \(MC \bot (ABD)\, \Rightarrow MC \bot AM\) ), từ đó\(\begin{array}{l}MC = \dfrac{{a\sqrt 3 }}{2},\,AC = \sqrt {4{a^2} + {a^2}} = a\sqrt 5 ,\\AM = \sqrt {4{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {17} }}{2}\\ \Rightarrow \,\,\tan \widehat {MAC} = \dfrac{{MC}}{{AM}} = \dfrac{{\sqrt 3 }}{{\sqrt {17} }} = \dfrac{{\sqrt {51} }}{{17}}\end{array}\).

Câu 9.

\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \)

Đáp án A không đủ dữ kiện để G là trọng tâm tứ diện ABCD.

Câu 10.

Ta có \(SG \subset \left( {SAC} \right),GS \bot \left( {ABCD} \right) \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\) , do đó góc giữa hai mặt phẳng (SAC) và (ABCD) là 90⁰. Chọn đáp án D.

xemloigiai.com