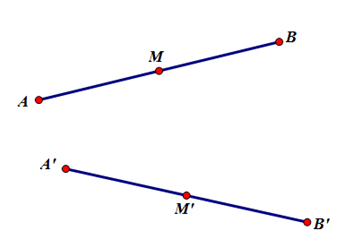
Câu hỏi 3 trang 21 SGK Hình học 11Gọi A’, B’ lần lượt là ảnh của A, B qua phép dời hình F. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.... Đề bài Gọi \(A’, B’\) lần lượt là ảnh của \(A, B\) qua phép dời hình \(F\). Chứng minh rằng nếu \(M\) là trung điểm của \(AB\) thì \(M’ = F(M)\) là trung điểm của \(A’B’.\) Phương pháp giải - Xem chi tiết +) Phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì. +) Biến ba điểm thằng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy. Quảng cáo  Lời giải chi tiết
Gọi \(A', B', M'\) lần lượt là ảnh của \(A, B, M\) qua phép dời hình \(F\) Theo tính chất 1 ta có: \(AB = A'B'\) và \(AM = A'M'\); Ba điểm \(A' B', M'\) thẳng hàng, trong đó \(M'\) nằm giữa. \(M\) là trung điểm \(AB ⇒ AM = {1 \over 2} AB\) Kết hợp (1) \(⇒ A'M' = {1 \over 2} A'B' ⇒ M'\) là trung điểm \(A'B'.\) xemloigiai.com
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
