Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho điểm \(M(1;2;3)\). Gọi \((P)\) là mặt phẳng đi qua điểm \(M\) và cách gốc tọa độ \(O\) một khoảng lớn nhất, mặt phẳng \((P)\) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp \(O \cdot ABC\).
- A \(\frac{{524}}{3}\).
- B \(\frac{{686}}{9}\).
- C \(\frac{{343}}{9}\).
- D \(\frac{{1372}}{9}\).
Phương pháp giải:
+ O.ABC có OA, OB, OC đôi một vuông góc với nhau thì hình chiếu của O lên (ABC) là trực tâm của tam giác ABC và có thể tích \({V_{O.ABC}} = \frac{1}{6}.OA.OB.OC\).
+ Tìm (P).
+ Tìm OA, OB, OC.
+ thể tích \({V_{O.ABC}} = \frac{1}{6}.OA.OB.OC\).
Lời giải chi tiết:
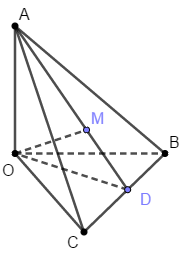
Ta có \(d{\left( {O,\left( P \right)} \right)_{\max }} \Leftrightarrow d\left( {O,\left( P \right)} \right) = OM\). Hay \(OM \bot \left( P \right) \equiv \left( {ABC} \right)\)
Mà OA, OB, OC đôi một vuông góc với nhau.
Suy ra M là trực tâm tam giác ABC.
\(\begin{array}{l} = > \left( P \right):1\left( {x - 1} \right) + 2\left( {y - 2} \right) + 3\left( {z - 3} \right) = 0\\ \Leftrightarrow x + 2y + 3z - 14 = 0\end{array}\)
Giả sử \(A \in Ox = > A\left( {a;0;0} \right) = > a = 14 = OA\)
Tương tự ta có \(OB = 7;OC = \frac{{14}}{3}\).
=> \({V_{O.ABC}} = \frac{1}{6}.OA.OB.OC = \frac{{686}}{9}\).













