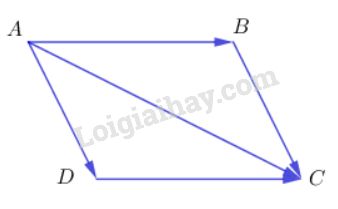
Bài 8 trang 29 SGK Hình học 10

Đề bài

Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây là đúng?

A. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \)

B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \)

C. \(\overrightarrow {AC} - \overrightarrow {BD} = 2\overrightarrow {CD} \)

D. \(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {CD} \)

Lời giải chi tiết

Ta có: tứ giác \(ABCD\) là hình bình hành nên: \(\left\{ \matrix{\overrightarrow {AB} = \overrightarrow {DC} \hfill \cr \overrightarrow {AD} = \overrightarrow {BC} \hfill \cr} \right.\)

+) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} +\overrightarrow {AD}+ \overrightarrow {BC} + \overrightarrow {BA}\)\( = 2\overrightarrow {BC}\) nên A đúng.

+) \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {BC}\)\( = \overrightarrow {AB} + 2\overrightarrow {BC} \ne \overrightarrow {AB} \) nên B sai.

+) \(\overrightarrow {AC} - \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {BC} - \overrightarrow {CD}\)

\(= \overrightarrow {AB} + \overrightarrow {DC} =\overrightarrow {DC}+\overrightarrow {DC}= 2\overrightarrow {DC} \ne 2\overrightarrow {CD} \) nên C sai.

+) \(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {DC} \ne \overrightarrow {CD} \) nên D sai.

Vậy A đúng.

Chú ý:

Có thể giải thích câu A và C bằng cách sử dụng điểm O là giao điểm hai đường chéo như sau:

\(\begin{array}{l}
+ )\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {OC} + 2\overrightarrow {BO} \\
= 2\left( {\overrightarrow {OC} + \overrightarrow {BO} } \right) = 2\left( {\overrightarrow {BO} + \overrightarrow {OC} } \right)\\
= 2\overrightarrow {BC} \\
+ )\overrightarrow {AC} - \overrightarrow {BD} = 2\overrightarrow {OC} - 2\overrightarrow {OD} \\
= 2\left( {\overrightarrow {OC} - \overrightarrow {OD} } \right) = 2\overrightarrow {DC}
\end{array}\)

xemloigiai.com