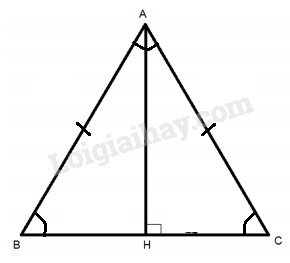
Bài 7 trang 63 SGK Hình học 10

Đề bài

Tam giác đều \(ABC\) có đường cao \(AH\). Khẳng định nào sau đây là đúng?

A. \(\sin \widehat {BAH} = {{\sqrt 3 } \over 2}\)

B. \(\cos \widehat {BAH} = {1 \over {\sqrt 3 }}\)

C. \(\sin \widehat {ABC} = {{\sqrt 3 } \over 2}\)

D. \(\sin \widehat {AHC} = {1 \over 2}\)

Lời giải chi tiết

Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác góc A.

\(\begin{array}{l}
\Rightarrow \widehat {BAH} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}{.60^0} = {30^0}\\
\Rightarrow \sin \widehat {BAH} = \sin {30^0} = \frac{1}{2}\\
\Rightarrow A\,sai\\
\cos \widehat {BAH} = \cos {30^0} = \frac{{\sqrt 3 }}{2}\\
\Rightarrow B\,sai\\
\sin \widehat {ABC} = \sin {60^0} = \frac{{\sqrt 3 }}{2}\\
\Rightarrow C\,\text{đúng}\\
\sin \widehat {AHC} = \sin {90^0} = 1\\
\Rightarrow D\,sai
\end{array}\)

Chọn C

xemloigiai.com