Bài 5 trang 27 (Ôn tập chương I - Vectơ) SGK Hình học 10Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho: Lựa chọn câu để xem lời giải nhanh hơn Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\). Hãy xác định các điểm \(M, N, P\) sao cho: LG a \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) Lời giải chi tiết:
Kéo dài \(OC\) cắt đường tròn tại điểm \(M\). MC là đường kính nên \(\widehat {MBC} = {90^0} \Rightarrow MB \bot BC\). Mà tam giác ABC đều nên \(AO\bot BC\). Do đó MB//OA (1) Lại có \(\widehat {MAC} = {90^0} \Rightarrow MA \bot AC\). Mà tam giác ABC đều nên \(BO\bot AC\). Do đó MA//BO (2) Từ (1) và (2) suy ra \(OAMB\) là hình bình hành, suy ra: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OM} \). Vậy M là điểm cần tìm. Cách 2: O là tâm tam giác ABC nên cũng là trọng tâm tam giác. Ta có: \(\begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = - \overrightarrow {OC} \end{array}\) Mà \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) Nên \(\overrightarrow {OM} = - \overrightarrow {OC} \) \( \Rightarrow \overrightarrow {OM} \) là véc tơ đối của \(\overrightarrow {OC} \) hay O là trung điểm của CM. Mà OC là bán kính nên CM=2CO là đường kính của đường tròn. Vậy M là giao điểm của CO với đường tròn. Cách 3: \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) \( \Leftrightarrow \) M là đỉnh còn lại của hình bình hành AOBM. + AOBM là hình bình hành ⇒ AM = OB Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1) + AOBM là hình bình hành ⇒ AM//BO \(\begin{array}{l} \Rightarrow \widehat {MAO} + \widehat {AOB} = {180^0}\\ \Leftrightarrow \widehat {MAO} + {120^0} = {180^0}\\ \Rightarrow \widehat {MAO} = {60^0}\,\,\left( 2 \right)\end{array}\) Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC. Mà \(\widehat {AOM} = \widehat {BOM}\) nên M là điểm chính giữa cung AB. LG b \(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \) Lời giải chi tiết: Nối \(OA\) và kéo dài cắt đường tròn tại điểm \(N\) Tương tự như trên ta có: \(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \) Cách khác: \(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \) \( \Leftrightarrow \) N là đỉnh còn lại của hình bình hành BOCN. + BOCN là hình bình hành ⇒ OB=CN Mà OB = OC (= bán kính đường tròn) ⇒ CN = CO ⇒ ΔCNO cân tại C (1) + BOCN là hình bình hành ⇒ CN//BO \(\begin{array}{l} \Rightarrow \widehat {NCO} + \widehat {BOC} = {180^0}\\ \Leftrightarrow \widehat {NCO} + {120^0} = {180^0}\\ \Rightarrow \widehat {NCO} = {60^0}\,\,\left( 2 \right)\end{array}\) Từ (1) và (2) ⇒ ΔCNO đều ⇒ ON = OC ⇒ N nằm trên đường tròn ngoại tiếp ΔABC. Mà \(\widehat {BON} = \widehat {CON}\) nên N là điểm chính giữa cung BC. LG c \(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \) Lời giải chi tiết: Nối \(OB\) và kéo dài cắt đường tròn tại điểm \(P\) Tương tự như trên ta có: \(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \) Cách khác: \(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \) \( \Leftrightarrow \) P là đỉnh còn lại của hình bình hành AOCP. + AOCP là hình bình hành ⇒ OA=PC Mà OA = OC (= bán kính đường tròn) ⇒ OC = PC ⇒ ΔCPO cân tại C (1) + AOCP là hình bình hành ⇒ AO//CP \(\begin{array}{l} \Rightarrow \widehat {PCO} + \widehat {COA} = {180^0}\\ \Leftrightarrow \widehat {PCO} + {120^0} = {180^0}\\ \Rightarrow \widehat {PCO} = {60^0}\,\,\left( 2 \right)\end{array}\) Từ (1) và (2) ⇒ ΔCPO đều ⇒ OP = OC ⇒ P nằm trên đường tròn ngoại tiếp ΔABC. Mà \(\widehat {AOP} = \widehat {COP}\) nên P là điểm chính giữa cung AC. xemloigiai.com
|













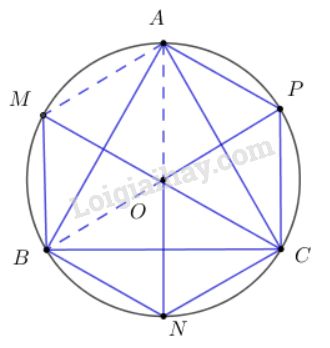 Cách 1:
Cách 1: 