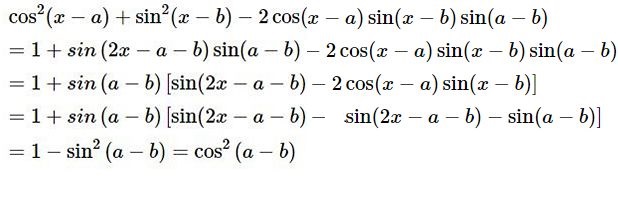Bài 1.60 trang 18 SBT Đại số và Giải tích 11 Nâng cao

Đề bài

Chứng minh rằng

\({\cos ^2}(x - a) + {\sin ^2}(x - b) \)\(- 2\cos (x - a)\sin (x - b)\sin (a - b) \)\(= {\cos ^2}(a - b)\)

Quảng cáo

Lời giải chi tiết

Ta có:

\(\eqalign{
& {\cos ^2}(x - a) + {\sin ^2}(x - b) \cr&= {{1 + \cos 2\left( {x - a} \right)} \over 2} + {{1 - \cos 2\left( {x - b} \right)} \over 2} \cr 
& = 1 + {1 \over 2}\left[ {\cos 2\left( {x - a} \right) - \cos 2\left( {x - b} \right)} \right] \cr& = 1 + \frac{1}{2}.\left( { - 2} \right)\sin \left( {2x - a - b} \right)\sin \left( {b - a} \right) \cr&= 1 - \sin \left( {2x - a - b} \right)\sin \left( {b - a} \right)\cr&= 1 + \sin \left( {2x - a - b} \right)\sin \left( {a - b} \right) \cr} \)

Do đó

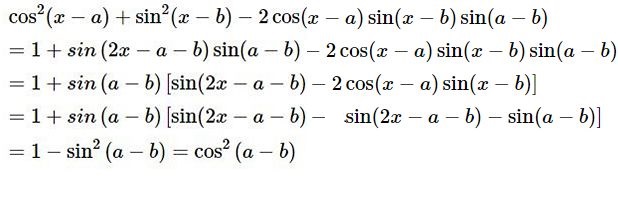
xemloigiai.com