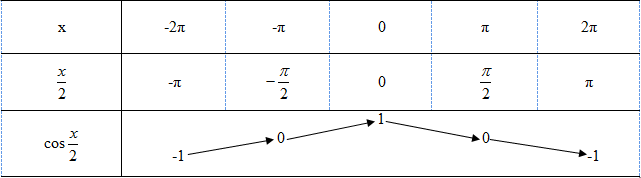
Câu 13 trang 17 SGK Đại số và Giải tích 11 Nâng cao

LG a

Chứng minh rằng với mỗi số nguyên $k$, $f(x + k4π) = f(x)$ với mọi $x$.

Lời giải chi tiết:

$f\left( {x + k4\pi } \right) = \cos \frac{{x + k4\pi }}{2}$

$= \cos \left( {{x \over 2} + k2\pi } \right)$ $= \cos {x \over 2} = f\left( x \right)$

Quảng cáo

LG b

Lập bảng biến thiên của hàm số $y = \cos {x \over 2}$ trên đoạn $[-2π ; 2π]$.

Lời giải chi tiết:

Bảng biến thiên :

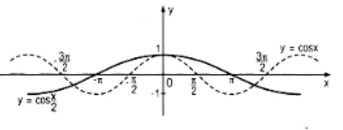
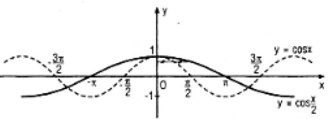
LG c

Vẽ đồ thị của các hàm số $y = \cos x$ và $y = \cos {x \over 2}$ trong cùng một hệ trục tọa độ vuông góc $Oxy$.

Lời giải chi tiết:

LG d

Trong mặt phẳng tọa độ $Oxy$, xét phép biến hình $F$ biến mỗi điểm $(x ; y)$ thành điểm $(x'; y')$ sao cho $x'= 2x$ và $y'= y$. Chứng minh rằng F biến đồ thị của hàm số $y = \cos x$ thành đồ thị của hàm số $y = \cos {x \over 2}.$

Lời giải chi tiết:

Ta có:

$\left\{ \begin{array}{l} x' = 2x\\ y' = y \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = \frac{{x'}}{2}\\ y =y' \end{array} \right.$

Do đó $y = \cos x$ $\Leftrightarrow$ $y' = \cos {{x'} \over 2}$.

Do đó phép biến đổi xác định bởi $(x ; y) ↦ (x' ; y')$ sao cho $x' = 2x, y'= y$ biến đồ thị hàm số $y = \cos x$ thành đồ thị hàm số $y = \cos {x \over 2}.$

 xemloigiai.com