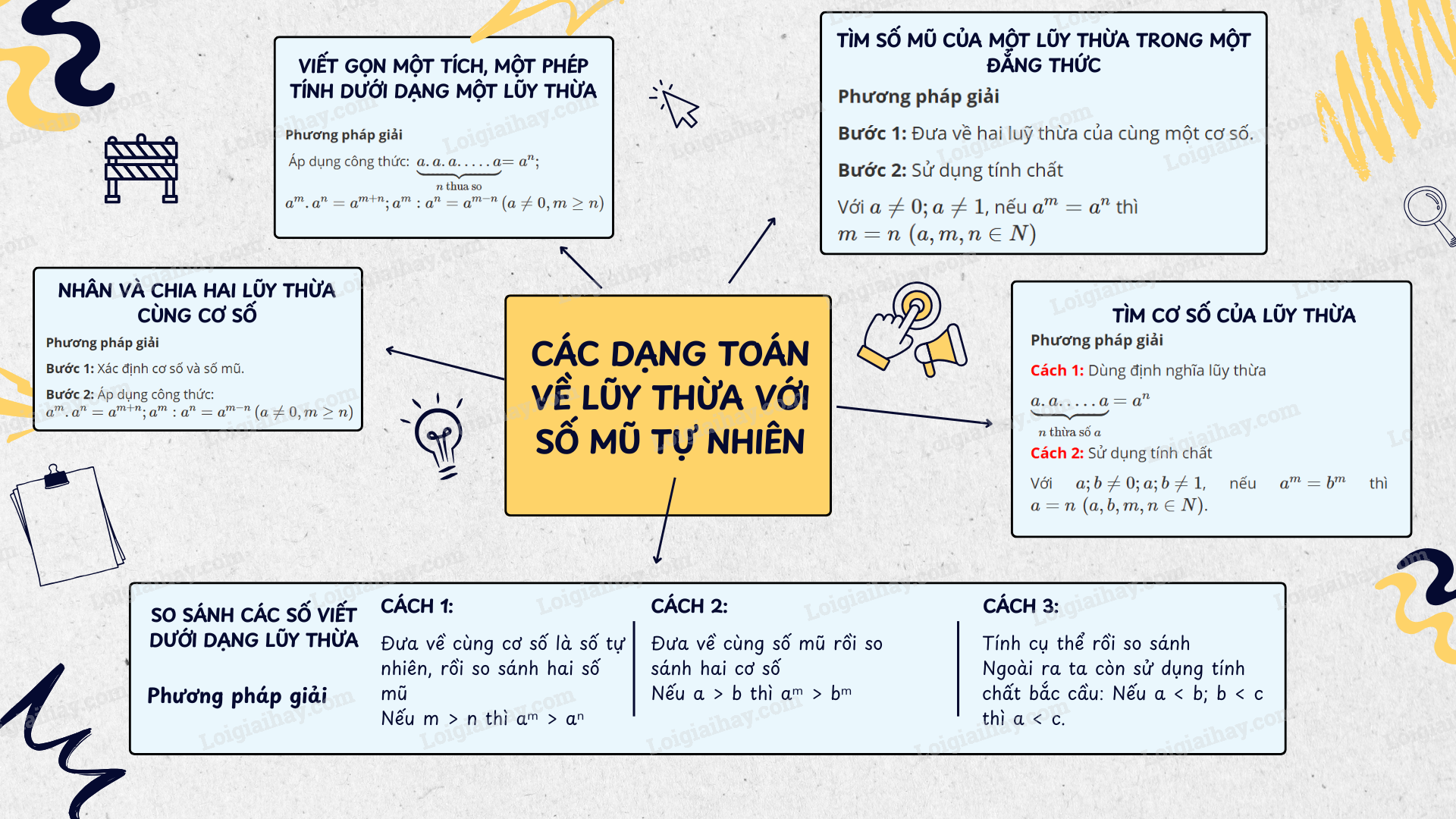
Các dạng toán về lũy thừa với số mũ tự nhiên

A. Các dạng bài tập

I. Viết gọn một tích, một phép tính dưới dạng một lũy thừa

Phương pháp giải

 Áp dụng công thức: $\underbrace {a.a.a.....a}_{n\,{\rm{thừa}}\,{\rm{số}}}$$ = {a^n};$${a^m}.{a^n} = {a^{m + n}};{a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0,m \ge n} \right)$

II. Nhân và chia hai lũy thừa cùng cơ số

Phương pháp giải

Bước 1: Xác định cơ số và số mũ.

Bước 2: Áp dụng công thức:${a^m}.{a^n} = {a^{m + n}};{a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0,m \ge n} \right)$

III. So sánh các số viết dưới dạng lũy thừa

Phương pháp giải

Để so sánh các số viết dưới dạng lũy thừa, ta có thể làm theo:

Cách 1: Đưa về cùng cơ số là số tự nhiên, rồi so sánh hai số mũ

Nếu \(m > n\) thì \({a^m} > {a^n}\)

Cách 2: Đưa về cùng số mũ rồi so sánh hai cơ số

Nếu \(a > b\) thì \({a^m} > {b^m}\)

Cách 3: Tính cụ thể rồi so sánh

Ngoài ra ta còn sử dụng tính chất bắc cầu: Nếu \(a < b;b < c\) thì \(a < c.\)

IV. Tìm số mũ của một lũy thừa trong một đẳng thức

Phương pháp giải

Bước 1: Đưa về hai luỹ thừa của cùng một cơ số.

Bước 2: Sử dụng tính chất 

Với \(a \ne 0;a \ne 1\), nếu ${a^m} = {a^n}$ thì $m = n\,\,(a,m,n \in N)$

V. Tìm cơ số của lũy thừa

Phương pháp giải

Cách 1: Dùng định nghĩa lũy thừa

$\underbrace {a.a.....a}_{n\,{\rm{thừa}}\,{\rm{số}}\,a}$ $ = {a^n}$
Cách 2: Sử dụng tính chất

Với \(a;b \ne 0;a;b \ne 1\), nếu ${a^m} = {b^m}$ thì $a = n\,\,(a,b,m,n \in N)$.

B. Bài tập vận dụng

Câu 1. Chọn câu sai.

A. \({a^m}.{a^n} = {a^{m + n}}\)

B. \({a^m}:{a^n} = {a^{m - n}}\) với $ m \ge n$ và $ a\ne 0$

C. \({a^0} = 1\)

D. \({a^1} = 0\)

Lời giải

Ta có với $ a,m,n \in N$ thì 

+ \({a^m}.{a^n} = {a^{m + n}}\) nên A đúng

+ \({a^m}:{a^n} = {a^{m - n}}\) với $ m \ge n$ và $ a\ne 0$ nên B đúng

+ $a^0=1$ nên C đúng.

+ \({a^1} = a\) nên D sai.

Đáp án D

Câu 2. Viết gọn tích \(4.4.4.4.4\) dưới dạng lũy thừa ta được

A. \({4^5}\)

B. \({4^4}\)

C. \({4^6}\)

D. \({4^3}\)

Lời giải

Ta có \(4.4.4.4.4 = {4^5}\)

Đáp án A

Câu 3. Viết tích \({a^4}.{a^6}\) dưới dạng một lũy thừa ta được

A. \({a^8}\)

B. \({a^9}\)

C. \({a^{10}}\)

D. \({a^2}\)

Lời giải

Ta có \({a^4}.{a^6}\)\( = {a^{4 + 6}} = {a^{10}}\)

Đáp án C

Câu 4. Lũy thừa nào dưới đây biểu diễn thương \({17^8}:{17^3}\)?

A. \({5^{17}}\)

B. \({17^5}\)

C. \({17^{11}}\)

D. \({17^6}\)

Lời giải

Đáp án B

Câu 5. Chọn câu sai.

A. \({5^3} < {3^5}\)

B. \({3^4} > {2^5}\)

C. \({4^3} = {2^6}\)

D. \({4^3} > {8^2}\)

Lời giải

+) Ta có \({5^3} = 5.5.5 = 125\); \({3^5} = 3.3.3.3.3 = 243\) nên \({5^3} < {3^5}\) (A đúng)

+) \({3^4} = 3.3.3.3 = 81\) và \({2^5} = 2.2.2.2.2 = 32\) nên \({3^4} > {2^5}\) (B đúng)

+) \({4^3} = 4.4.4 = 64\) và \({2^6} = 2.2.2.2.2.2 = 64\) nên \({4^3} = {2^6}\) (C đúng)

+) \({4^3} = 64;{8^2} = 64\) nên \({4^3} = {8^2}\) (D sai)

Đáp án D

Câu 6. Tính \({2^4} + 16\) ta được kết quả dưới dạng lũy thừa là

A. \({2^{20}}\)

B. \({2^4}\)

C. \({2^5}\)

D. \({2^{10}}\)

Lời giải

Ta có \({2^4} + 16 = 2.2.2.2 + 16 = 16 + 16 = 32\) \( = 2.2.2.2.2 = {2^5}\).

Đáp án C

Câu 7. Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)

Lời giải

Ta có \({3^n} = 81\) mà \(81 = {3^4}\) nên \({3^n} = {3^4}\) suy ra \(n = 4.\)

Câu 8. Tìm số tự nhiên \(x\) thỏa mãn \({4^x} = {4^3}{.4^5}\)

Lời giải

Ta có \({4^x} = {4^3}{.4^5}\)

\({4^x} = {4^{3 + 5}}\)

\({4^x} = {4^8}\)

\(x = 8\)

Vậy \(x = 8.\)

Câu 9. Số tự nhiên \(m\) nào thỏa mãn \({20^{2018}} < {20^m} < {20^{2020}}?\)

Lời giải

Ta có \({20^{2018}} < {20^m} < {20^{2020}}\) suy ra \(2018 < m < 2020\) nên \(m = 2019.\)

Câu 10. Số tự nhiên \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = 125\) là

Lời giải

Ta có \({\left( {2x + 1} \right)^3} = 125\)

\({\left( {2x + 1} \right)^3} = {5^3}\)

\(2x + 1 = 5\)

\(2x = 5 - 1\)

\(2x = 4\)

\(x = 4:2\)

\(x = 2.\)

Vậy \(x = 2.\)