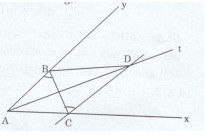
Bài tập 8 trang 156 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho góc xAy nhọn có At là tia phân giác. Trên tia At ta lấy điểm D, đường thẳng song song với Ay kẻ từ D cắt Ax tại C.

a) Chứng minh rằng $\widehat {CAD} = \widehat {CDA}$

b) Trên Ay, lấy điểm B sao cho AB = AC. Chứng minh rằng $\Delta ACD = \Delta ABD$

c) Chứng minh rằng AC = DB và AC // DB.

Lời giải chi tiết

a)Ay // DC (gt)$\Rightarrow \widehat {yAD} = \widehat {ADC}$ (hai góc so le trong).

Mà $\widehat {yAD} = \widehat {CAD}$ (At là tia phân giác góc xAy)

Do đó: $\widehat {CAD} = \widehat {ADC}$

b) Xét tam giác ACD và ABD có:

AC = AB (gt)

$\widehat {CAD} = \widehat {BAD}$ (At là tia phân giác của góc xAy)

AD là cạnh chung.

Do đó: $\Delta ACD = \Delta ABD(c.g.c)$

c) $Ay//CD \Rightarrow \widehat {ABC} = \widehat {DCB}$ (hai góc so le trong)

$\Delta ACD = \Delta ABD$ (chứng minh câu b) $\Rightarrow \widehat {ACD} = \widehat {ABD}$

Mà $\widehat {DBC} + \widehat {ABC} = \widehat {ABD};\widehat {ACB} + \widehat {BCD} = \widehat {ACD}.$ Nên $\widehat {DBC} = \widehat {ACB}$

Xét tam giác ABC và DCB có:

$\eqalign{ & \widehat {ABC} = \widehat {DCB}(cmt) \cr & \widehat {ACB} = \widehat {DBC}(cmt) \cr}$

BC là cạnh chung.

Do đó: $\Delta ABC = \Delta DCB(g.c.g) \Rightarrow AC = BD$

Ta có: $\widehat {DBC} = \widehat {BCA}$ (chứng minh trên)

Mà hai góc này ở vị trí so le trong nên BD // AC.

xemloigiai.com