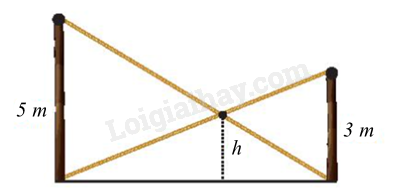
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 5 m và 3 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm. Tính độ cao ℎ của điểm đó so với mặt đất.

Cho tam giác ABC nhọn (AB < AC)  có hai đường cao BE, CF cắt nhau tại H

a) Chứng minh $\Delta ABE\backsim \Delta ACF$

b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).

c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.

Cho công thức \(C = \frac{5}{9}\left( {F - 32} \right)\) với C = 10. Tính \(F\), ta được kết quả:

Một mô hình ô tô dài 12cm. Thực tế ô tô dài 2,4m. Tỉ số đồng dạng của mô hình và vật thật là: