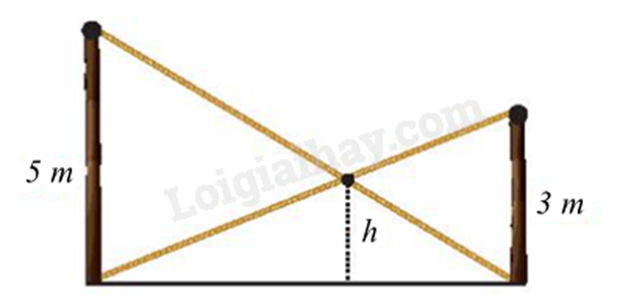
1. Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 5 m và 3 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm. Tính độ cao ℎ của điểm đó so với mặt đất.
2. Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H
a) Chứng minh $\Delta ABE\backsim \Delta ACF$
b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).
1. - Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h.
2. a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc.
b) Chứng minh $\Delta HED\backsim \Delta HCE$ suy ra tỉ số đồng dạng, ta được điều phải chứng minh.
1. 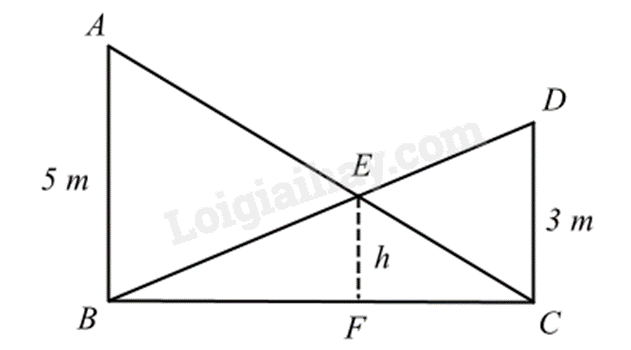
Ta có: AB // CD nên \(\widehat {BAC} = \widehat {DCA}\) và \(\widehat {ABD} = \widehat {CDB}\) (hai góc so le trong)
Xét \(\Delta ABE\) và \(\Delta CDE\) có:
\(\begin{array}{l}\widehat {BAC} = \widehat {DCA}\\\widehat {ABD} = \widehat {CDB}\end{array}\)
Suy ra $\Delta ABE\backsim \Delta CDE$ (gg)
Suy ra \(\frac{{CE}}{{AE}} = \frac{{CD}}{{AB}} = \frac{3}{5}\)
Suy ra \(\frac{{CE}}{{AC}} = \frac{3}{8}\)
Xét \(\Delta CFE\) và \(\Delta CBA\) có:
\(\widehat C\) chung
\(\widehat {ABC} = \widehat {EFC}\)
suy ra $\Delta CFE\backsim \Delta CBA$ (g.g)
suy ra \(\frac{{EF}}{{AB}} = \frac{{CE}}{{AC}} = \frac{3}{8}\). Do đó \(EF = \frac{3}{8}.AB = \frac{3}{8}.5 = \frac{{15}}{8}\) (m)
2.
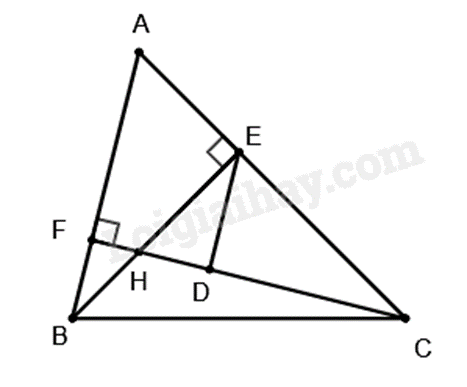
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {BEA} = \widehat {CFA} = {90^0}\)
\(\widehat A\) chung
suy ra $\Delta ABE\backsim \Delta ACF$ (g.g) (đpcm)
b) Ta có DE // AB nên \(\widehat {HED} = \widehat {ABE}\) (hai góc so le trong)
\(\widehat {ACF} = \widehat {ABE}\) (do $\Delta ABE\backsim \Delta ACF$)
suy ra \(\widehat {ACF} = \widehat {HED}\)
Xét \(\Delta HED\) và \(\Delta HCE\) có:
\(\widehat H\) chung
\(\widehat {ACF} = \widehat {HED}\)
suy ra $\Delta HED\backsim \Delta HCE$ (g.g)
suy ra \(\frac{{HE}}{{HC}} = \frac{{HD}}{{HE}}\) hay \(H{E^2} = HD.HC\) (đpcm)
Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \(x + 2 = - 6x + 16\)
b) \(2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8\)
c) \(\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2\)
d) \(\frac{{2x + 1}}{3} + \frac{{3x - 2}}{2} = \frac{1}{6}\)
Cho ba số thực a, b, c khác 2 thỏa mãn a + b + c = 6. Tính giá trị của biểu thức:
\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)
Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Gọi x là tuổi của Phương năm nay vậy thì phương trình tìm x là
Lớp 8B có 40 học sinh trong đó có 18 học sinh nữ. Lớp phó lao động chọn một bạn để trực nhật trong một buổi học. Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp trong buổi học” là:
Cho tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng là 2. Tam giác DEF đồng dạng với tam giác MNP theo tỉ số đồng dạng là 2. Biết \(\widehat A = {30^0}\), tính số đo \(\widehat M\)
Tam ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Biết chu vi tam giác MNP là 12cm, chu vi tam giác ABC là:












