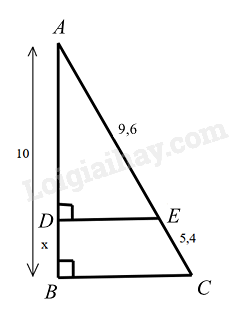
Cho hình vẽ sau, giá trị của x là:
- A. 6,4.
- B. 3,6.
- C. 17,7.
- D. 5,6.
Đáp án : B
Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm x.
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat B = \widehat D = {90^0}\)
\(\widehat A\) chung
Suy ra $\Delta ABC\backsim \Delta ADE$ (g.g)
Do đó \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DE}}\) hay \(\frac{{10}}{{9,6 + 5,4}} = \frac{{AD}}{{9,6}}\)
Suy ra \(AD = 9,6.\frac{{10}}{{9,6 + 5,4}} = 6,4\)
Vậy \(x = AB - AD = 10 - 6,4 = 3,6\).
Đáp án B.
Các bài tập cùng chuyên đề
1. Giải các phương trình sau:
a) \(3\left( {x - 1} \right) - 7 = 5\left( {x + 2} \right)\)
b) \(\frac{{x + 4}}{5} - x + 4 = \frac{x}{3} - \frac{{x - 2}}{2}\)
2. Cho hàm số \(\left( d \right):y = \left( {m - 1} \right)x + 4\) (m là tham số, \(m \ne 1\)).
a) Tìm m để đường thẳng (d) song song với đường thẳng \(\left( {{d_1}} \right):y = 3 - 2x\).
b) Tìm m để đường thẳng (d) cắt đường thẳng \(\left( {{d_2}} \right):y = x + m\) tại một điểm nằm trên trục tung.
Giải bài toán bằng cách lập phương trình
Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 7m. Nếu tăng chiều rộng lên gấp 3 lần và tăng chiều dài thêm 5m thì mảnh đất trở thành hình vuông. Tính diện tích mảnh đất hình chữ nhật lúc đầu.
1. Khu bảo tồn Muttart là một phần biểu tượng của cảnh quan thành phố Edmonton, Canada với bốn nhà kính dạng kim tự tháp. Mỗi tòa nhà đều có từng chủ đề riêng. Hai nhà kính lớn đều có dạng hình chóp tứ giác đều với chiều cao 24m và diện tích đáy mỗi nhà kính khoảng \(660{m^2}\). Tính tổng thể tích hai nhà kính này.

2. Cho \(\Delta ABC\) nhọn (AB < AC). Hai đường cao BE và CF.
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ và \(AE.AC = AF.AB\)
b) Trên tia BE lấy điểm N sao cho \(\widehat {ANC} = {90^0}\) (E nằm giữa B và N). Chứng minh $\Delta ANE\backsim \Delta ACN$ và \(A{N^2} = AE.AC\).
c) Trên cạnh CF lấy điểm M sao cho AM = AN. Tính số đo \(\widehat {AMB}\).
Số học sinh tham gia Câu lạc bộ Cờ tướng của một trường được biểu diễn ở biểu đồ sau:
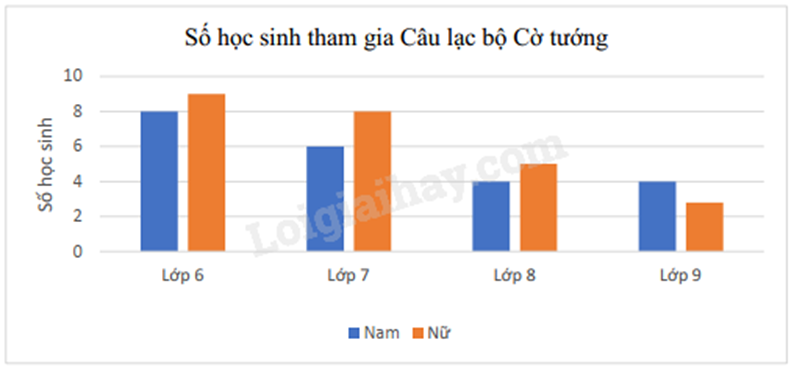
Chọn ngẫu nhiên 1 học sinh Câu lạc bộ Cờ tướng của trường đó. Tính xác suất của biến cố “Học sinh được chọn là nam và không học lớp 7”.
Giải phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\).
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
Giá trị của m để đường thẳng \(y = \left( {m - 3} \right)x - 1 + m\) và đường thẳng \(y = x + 1\) song song với nhau là:
Bạn An tung một đồng xu cân đối và đồng chất 20 lần, có 9 lần mặt ngửa, 11 lần mặt sấp. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là:
Một hộp có 10 tấm thẻ cùng loại được đánh số từ 5 đến 14. Bạn An lấy ra ngẫu nhiên 1 thẻ từ hộp. Xác suất của biến cố “Chọn ra thẻ ghi số chia hết cho 5” là bao nhiêu phần trăm?
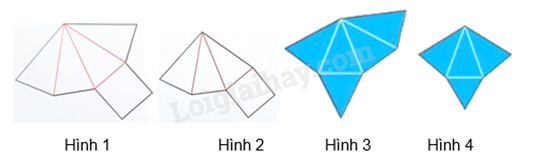
Trong các miếng bìa sau, miếng bìa nào khi gấp và dán lại thì được một hình chóp tứ giác đều?
Tính thể tích khối rubik có dạng hình chóp tam giác đều (hình bên). Biết khối rubik này có bốn mặt là các tam giác đều bằng nhau cạnh 5,2cm và chiều cao của tam giác là 4,5cm; chiều cao của khối rubik bằng 4,2cm.