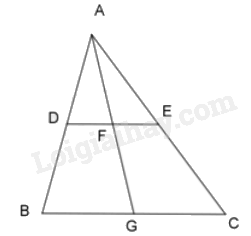
Cho tứ giác \({\rm{ABCD}}\) có \({\rm{AC}}\) và \({\rm{BD}}\) cắt nhau tại \({\rm{O}}\). Qua \({\rm{O}}\), kẻ đường thẳng song song với \({\rm{BC}}\) cắt \({\rm{AB}}\) tại \({\rm{E}}\), kẻ đường thẳng song song với \({\rm{CD}}\) cắt \({\rm{AD}}\) tại \({\rm{F}}\).
a) Chứng minh \({\rm{FE}}//{\rm{BD}}\);
b) Từ \(O\) kẻ đường thẳng song song với \(AB\) cắt \(BC\) tại \(G\) và đường thẳng song song với \(AD\) cắt \(CD\) tại \(H\) . Chứng minh rằng CG.DH = BG.CH.
Định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Định lí Thales đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
a) Xét \(\Delta ADC\) có \(OF//DC\), theo định lí Thales suy ra \(\frac{{AF}}{{AD}} = \frac{{AO}}{{AC}}\left( 1 \right)\)
Xét \(\Delta ABC\) có \(OE//BC\), theo định lí Thales ta có \(\frac{{AE}}{{AB}} = \frac{{AO}}{{AC}}\left( 2 \right)\)
Từ (1),(2) suy ra \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\)
Theo định lí Thales đảo trong \(\Delta ADB\) có: \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AB}}\) suy ra \(EF//BD\left( {{\rm{dpcm}}} \right)\)
b) Xét \(\Delta ADC\) có \(OH//AD\), theo định lí Thales ta có \(\frac{{CH}}{{CD}} = \frac{{CO}}{{AC}}\left( 3 \right)\)
Xét \(\Delta ABC\) có \(OG//AB\), theo định lí Thales ta có \(\frac{{CG}}{{BC}} = \frac{{CO}}{{AC}}\left( 4 \right)\)
Từ (3),(4) suy ra \(\frac{{CH}}{{CD}} = \frac{{CG}}{{BC}}\)
Theo định lí Thales đảo suy ra \(GH//BD\).
Xét \(\Delta BCD\) có \(GH//BD\), theo định lí Thales ta có \(\frac{{CH}}{{DH}} = \frac{{CG}}{{BG}}\) suy ra \(CH \cdot BG = DH \cdot CG\left( {{\rm{dpcm}}} \right)\).
Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \(\frac{x}{2} - \frac{1}{5} = 2 - \frac{x}{3}\)
b) \(1 - \frac{{x + 5}}{3} = \frac{{3\left( {x - 1} \right)}}{4}\);
c) \(\frac{{6\left( {x - 2} \right)}}{7} - 12 = \frac{{2\left( {x - 7} \right)}}{3}\)
Năm ngoái, tổng số công nhân của hai phân xưởng là 270 người. Năm nay, số công nhân của phân xưởng I tăng \(5{\rm{\% }}\), số công nhân của phân xưởng II tăng \(6{\rm{\% }}\) nên tổng số công nhân của hai phân xưởng là 285 người. Hỏi năm nay, mỗi phân xưởng có bao nhiêu công nhân?
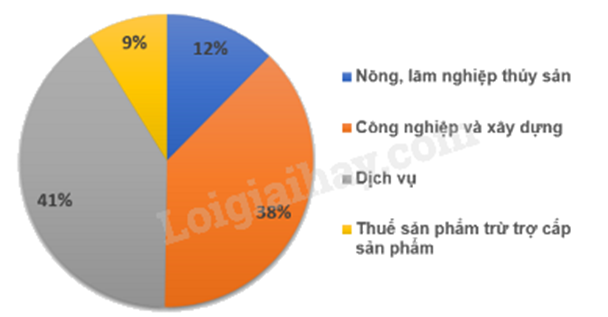
Cho biểu đồ hình quạt trong biểu diễn cơ cấu GDP của Việt Nam năm 2021.
Lĩnh vực nào đóng góp nhiếu nhất vào GDP, với bao nhiêu phần trăm?
GDP Việt Nam năm 2021 là 0,4 nghìn tỉ đô la Mỹ. Lĩnh vực dịch vụ đóng góp bao nhiêu tỉ đô la Mỹ?
Gieo con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau:

Tính xác suất của thực nghiệm của biến cố "Mặt xuất hiện là mặt 4".
Tính xác suất của thực nghiệm của biến cố "Mặt xuất hiện có số chấm là số chẵn chia hết cho 3".
Tính xác suất của thực nghiệm của biến cố "Mặt xuất hiện có số chấm là số lẻ và là ước của 6".
Giải phương trình \(\frac{{7 - 2x}}{2} - \frac{2}{5}\left( {2 - x} \right) = 1\frac{1}{4}\) ta được:
Để biểu diễn tỉ lệ phần trăm của mỗi đối tượng trong tổng thể ta dùng biểu đồ nào sau đây?
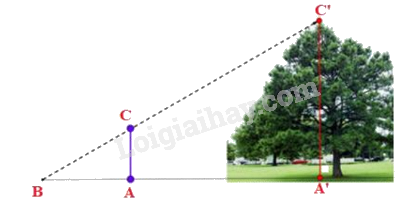
Hình dưới đây mô tả cách đo chiều cao của cây. Các thông số đo đạc được như sau: \(AB = 1m;AA' = 4,5m;CA = 1,2m\). Chiều cao của cây là
Cho hình thoi \(ABCD\) có \(M\) là trung điểm của \(AD\), đường chéo \(AC\) cắt \(BM\) tại điểm \(E\).
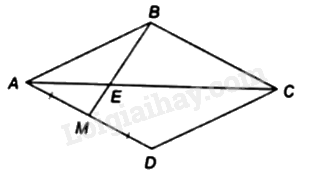
Tỉ số \(\frac{{EM}}{{EB}}\) bằng:
Tìm tất cả các số thực a sao cho \(x = 4\) là một nghiệm của phương trình:
\(x + 2a = 16 + ax - 6a\)
Một hộp có 1 quả bóng vàng, 1 quả bóng hồng và 1 quả bóng đỏ; các quả bóng có kích thước và khối lượng như nhau . Mỗi lần lấy ngẫu nhiên 1 quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Trong 45 lần lấy bóng liên tiếp, quả bóng vàng xuất hiện 5 lần; quả bóng hồng xuất hiện 10 lần. Tính xác suất thực nghiệm của biến cố "Quả bóng lấy ra là quả bóng màu đỏ".
Cho hình sau, biết giữa hai điểm \(B\) và \(C\) có một hồ sâu. Khoảng cách giữa hai điểm \(D\) và \({\rm{E}}\) đo được là \(53{\rm{\;m}}\). Hỏi \({\rm{B}}\) và \({\rm{C}}\) cách nhau bao nhiêu mét?
Bạn An đi bộ với vận tốc không đổi trong 45 phút trước khi chạy bộ trong nửa giờ với vận tốc gấp đôi vận tốc đi bộ. Bạn An di chuyển được quãng đường tổng cộng dài \(7{\rm{\;km}}\). Tính vận tốc đi bộ của bạn An.
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1;3;5; \ldots ;97\); 99; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố: "Số xuất hiện trên thẻ được rút ra là số lớn hơn 3 và là ước của 50 "